Heeei ♥ Jeg tror faktisk ikke kommer på noen ting som passer bedre enn en ny runde Ukens Formel! (Blant annet fordi at hvis jeg ikke skriver om ukens formel nå før vi går over i mandag, så har jeg feilet på å ha en formel i uken allerede på første forsøk, og det er så innmari kjedelig... :P).
Denne uken fortsetter jeg med noe som er viktig for oss som jobber med radioaktive ting, nemlig halveringstidsformelen. Eller, egentlig er det formelen for eksponensielt henfall, og gjelder for alle ting som minker eksponensielt:

Det denne formelen sier er at hvis du starter med å ha et visst antall av et eller annet, som vi kaller for N0, og halveringstiden til dette et eller annet er t1/2 , så kan vi regne ut hvor mye som er igjen etter at det har gått så og så lang tid t. Vi kaller det N0, siden N er en bokstav ofte brukes som antall av noe, og dette er så mye vi har når det har gått 0 tid (helt i starten).
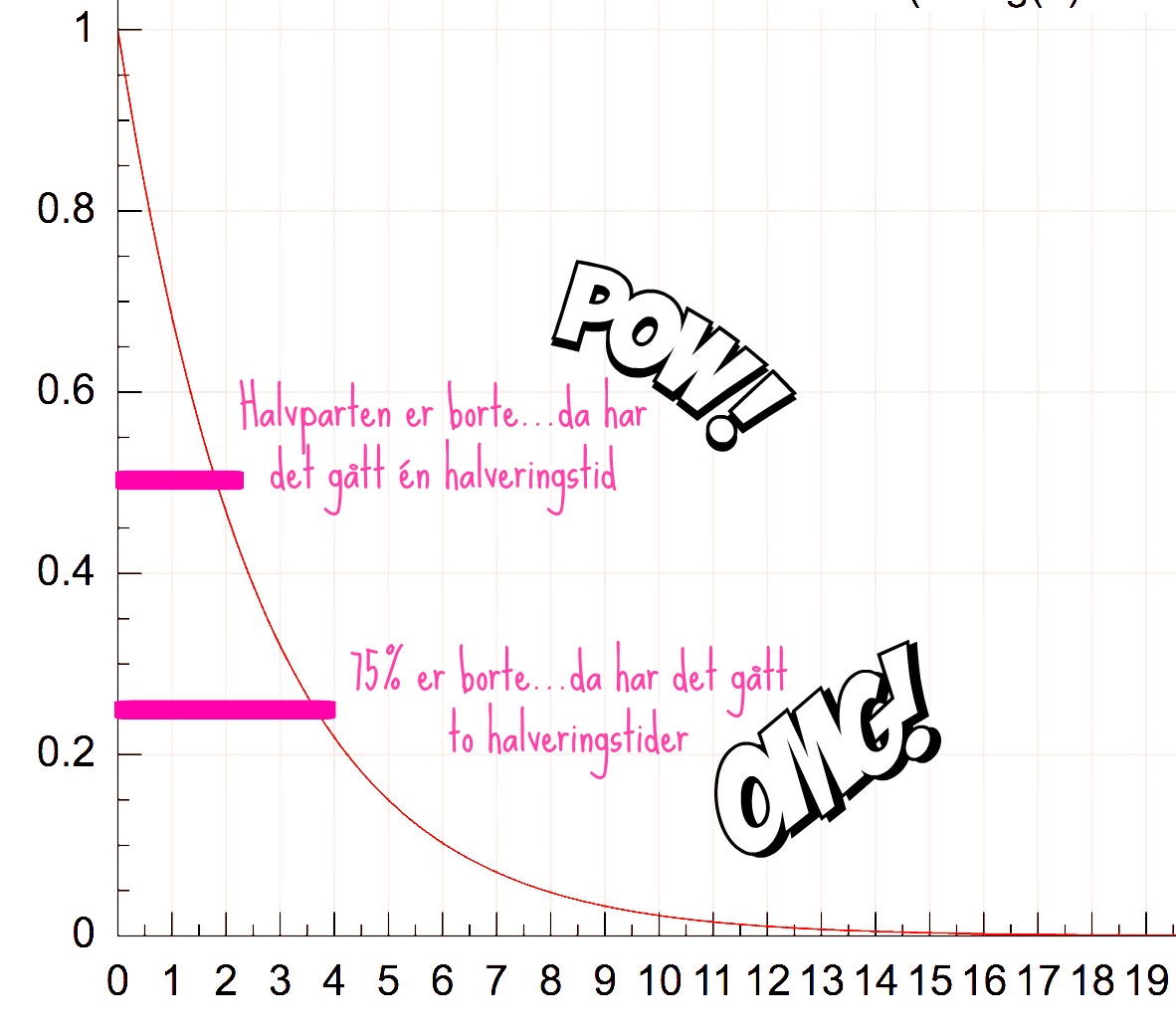
Etter én halveringstid så er halvparten borte, etter to halveringstider har vi mistet halvparten av det igjen - dvs 3/4 borte, osv. Etter 7 halveringstider er det bare 1/128 igjen, eller, altså mindre enn 1%. En tommelfingerregel er at man sier at da er "alt" borte - noe som egentlig betyr at det er så lite igjen av det man opprinnelig hadde at man kan regne med at resten ikke har noe å si (det er selvsagt ikke sant hvis man har noe som er veldig radioaktivt, eller man har veldig store mengder av det opprinnelig; 1% av noe som er veldig mye kan jo fremdeles være ganske masse).
I litt mer detalj:
Man starter altså med N0 atomer - f. eks. 1000 (dette er et latterlig lavt tall, men det er enkelt og fint og greit og pent å forholde seg til, syns jeg :)). Halveringstiden til dette atomet er for eksempel 2 sekunder - t1/2 er dermed 2. Hvis man lurer på hvor mange atomer det er igjen etter det har gått tid, for eksempel 8 sekunder, så kan man putte inn i formelen. Vi finner først hvor mange halveringstider det har gått
\(\frac{t}{t_{1/2}} = \frac{8}{2} = 4\)og setter det inn i formelen
\(N = N_0\cdot\Big(\frac{1}{2}\Big)^4 = 1000\cdot 0.5\cdot 0.5\cdot 0.5\cdot 0.5 \\ \qquad\qquad = 1000\cdot 0.0625 = 62.5\)
Så hvis halveringstiden er 2 sekunder, og vi venter 8 sekunder har vi bare litt over 50 atomer igjen av de 1000 vi startet med!
Hvis man lurer på hvor mange atomer vi har igjen etter 3.3 sekunder (da har det jo ikke gått et heltall antall halveringstider), så kan vi dytte formelen inn i Google omtrent som dette: http://lmgtfy.com/?q=1000*0.5%5E(3.3+%2F+2). Da ser vi at det er igjen omtrent 300 atomer.
Hvis vi ikke vet hva halveringstiden er, men noen har tegnet grafen for oss (enten fra eksperiment eller kanskje du har fått i oppgave å finne halveringstiden ved å se på grafen), så kan vi bare se på den øverste rosa streken (den er der y-aksen viser 0.5) og sjekke hvilken tid på x-aksen det svarer til. I denne grafen her ser vi at det er litt under 2, kanskje 1.8?
Formelen er som sagt ikke bare for å regne ut hvor mange atomer man har igjen etter en viss tid, men ser lik ut for alle ting som halveres på et eller annet vis. Feks er det gjerne halveringstykkelse når man ser på hvor tykk vegg av bly man trenger for å beskytte mot gamma-stråling, eller det er snakk om halveringstid av medisiner i kroppen (da er det nøyaktig det samme som formelen over), og sikkert mange andre ting som jeg ikke kommer på i farten 🙂
Hvis ikke alt var 100% superklart i denne teksten er det bare å spørre i kommentarfeltet, så skal jeg prøve å forklare så godt jeg kan ♥

Selv regner jeg ikke på halveringer, men mer på det å øke proporsjonalt med markedets kraft/evne/takt å må sette inn noe mer i formelen, men på samme måte some du regner deg ned tar jeg i bruk en lignende formel for å komme meg opp. G=((Bevegelse)Takt)-eller+, men det avhenger av markedet å hvilket bølger jeg antar å se. Mye av min formel må være diffus, men det er G for gevinst= (B for bevegelse) (opp i mot M for markedet lynne) sett i forhold til(T for takt) som avgjør utfallet, men her er det nært sagt umulig å sette det sammen før en før en følelse for spillet å en må noen ganger endre rekkefølge og sammensetning underveis for å komme ut med gevinst å noen ganger gir negativ retning gevinst(Short) andre ganger positiv(long), men prinsippet er så godt som likt selv om oppsettet mitt nok virker kaotisk fore aa si det mildt?men naa er det jeg driver med ett spill aa Oslo Børs blir ikke kalt Casino for ingenting!
så enig din lille khanzir
Åh, du skulle begynt med ukens formel litt tidligere haha, er nettopp ferdig med fysikk- og matte-fagene for en stund. Men er likevel greit å kunne gå tilbake og se hvis det trengs en anna gang:D
eow camilla slide lige din snap
kæft du en shabab, tak for at redde min opgave
Går ikke inn i hode mitt engang 🙁