Denne ukens formelfredag MÅ jo bli en liten oppsummering av forelesningen jeg holdt i nukleær teknologi tidligere i dag: Firefaktorformelen (som ved en feil først ble skrevet Fire4faktorformelen nå - og det er vel nesten sånn jeg burde fortsette å skrive den 😛 ). Vi bretter opp ermene, selv om det er fredag, og går rett på sak!
- oppskrift -
Firefaktorformelen er, som det vel nesten sier seg selv, en formel som består av fire faktorer - altså fire forskjellige tall/verdier som ganges sammen (faktorer er ting som ganges sammen). Den er enkel og grei på formen, og ikke vanskelig å bruke i det hele tatt, og den ser sånn ut:
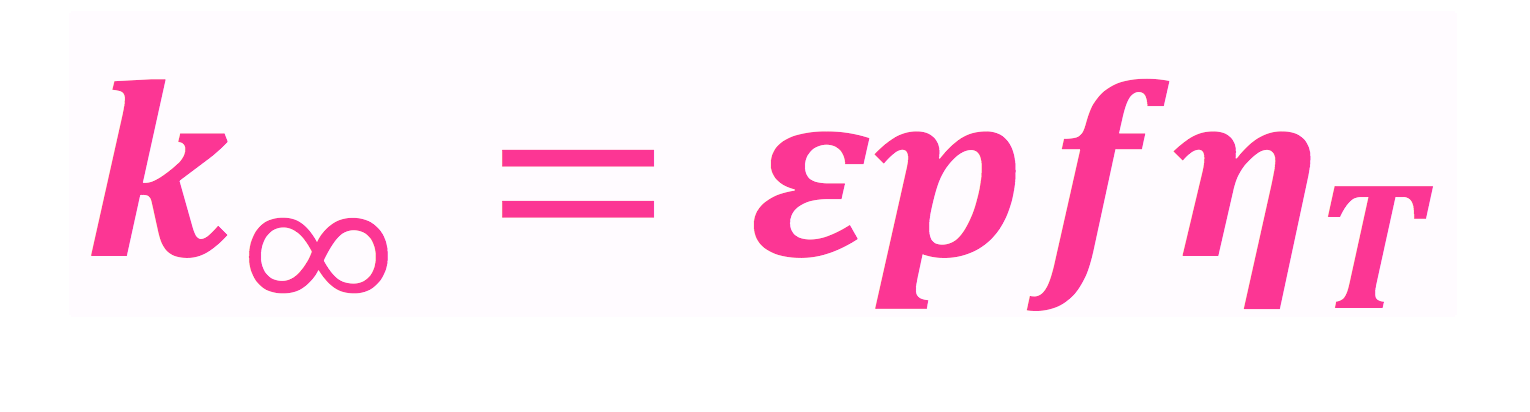
og med ord så blir det k uendelig \((k_\infty)\) er lik epsilon \((\epsilon)\) ganget med p ganget med f ganget med eta T \((\eta_T)\), for det står et usynlig gangetegn mellom faktorene, som man vanligvis ikke skriver. Jeg har faktisk ikke vært konsekvent på om jeg skriver gangetegn eller ikke her på bloggen innser jeg, for forrige ukes strekning og fart og tid skrev jeg med gangetegn, mens formelfredag for to uker siden, som handlet om Newtons andre lov, skrev jeg uten gangetegn... Vel vel, da er det i alle fall forklart, og det er lov å skrive uten å ta med gangetegnet 🙂
- hva det betyr -
På venstre siden av likhetstegnet står k uendelig, og dette kalles for nøytron-multiplikasjonsfaktoren (for en uendelig stor reaktor). For å holde tunga rett i munnen: nøytron-multiplikasjonsfaktoren forteller om det blir flere eller færre nøytroner i en reaktor, så det er altså forholdet mellom hvor mange nøytroner som fins etter den nåværende generasjonen med fisjon sammenliknet med hvor mange det var i forrige generasjon.
Hvis k er større enn 1 så betyr det at det skjer mer og mer fisjoner i brenselet, og reaktoren løper løpsk. Hvis k er akkurat 1 (som den skal) så er reaktoren kritisk, og det betyr at den er balansert og alt er fint og flott, og det er like mye fisjon som skjer hele tiden. Hvis k er mindre enn 1 så betyr det at det skjer mindre og mindre fisjon i brenselet, og hele kjedereaksjonen slutter og reaktoren skrur seg av.
På høyre side av likhetstegnet står det først \(\epsilon\), som er hvor mange nøytroner som vil gå rett og gi rask fisjon (fast fission factor), og dermed flere nøytroner totalt sett. Neste faktor er p, som er hvor mange nøytroner som blir spist opp av brenselet mens de egentlig skal bremses ned (resonance escape probability), så her blir det færre nøytroner. Faktor nummer tre er f, som forteller hvor mange termiske nøytroner som faktisk blir spist opp - så selv om nøytronene har overlevd til den energien som gir høyest sannsynlighet for fisjon så vil allikevel en god del bli spist opp i ikke-brensel (thermal utilization). Til slutt er det \(\eta_T\), som forteller hvor mange nøytroner man får for hvert nøytron som treffer en spaltbar kjerne, altså som treffer en kjerne i det som faktisk er brensel.
- fremgangsmåte -
Hvis vi starter med 1000 nøytroner, så skal det fortsette å være 1000 nøytroner totalt etter hver eneste generasjon med fisjoner i brenselet.
Eta kan feks være 1.04. Det betyr at det blir 1000 nøytroner ganget med 1.04 = 1040 nøytroner. Videre kan p være 0.8, som gjør at av de 1040 nøytronene er det bare 1040*0.8 = 832 som overlever det å bli bremset ned til lav energi. De andre blir "spist opp" av uran-238 (hovedsakelig) på veien. Deretter kan f være 0.799, som betyr at 832*0.799 = 655 - altså at det er 655 nøytroner som faktisk gir fisjon i brenselet. De andre nøytronene (832-655 = 167) blir "spist opp" av kjølevæske og kontrollstaver og uran-238 (forskjellen fra den forrige faktoren er at nå er det snakk om de nøytronene som har fått riktig energi, mens den forrige faktoren handler om hva som skjer på veien fra høy energi til riktig, lav energi), som altså ikke fisjonerer. Den siste faktoren er \(\eta_T\), som forteller hvor mange nøytroner som kommer ut for hvert nøytron som går inn i en fissil kjerne (altså uran-235). \(\eta_T\) er faktisk ikke det det samme som hvor mange nøytroner man får fra hver eneste fisjon, for \(\eta_T\) tar også med i beregningen at en liten del av de nøytronene som treffer uran-235-kjernen vil bli spist opp, og noen vil gjøre andre ting. Hvis \(\eta_T\) = 2.02 blir det 655*2.02 = 1323 nøytroner.
1323 er åpenbart mer enn de 1000 som var til å begynne med, så det kan virke som om de tallene jeg har satt opp gir en kjedereaksjon som løper løpsk. MEN! Firefaktorformelen tar ikke med en siste, viktig faktor - nemlig hvor mange nøytroner som forsvinner ut av reaktoren (det er ikke så lett å passe på alle nøytronene hele tiden). Det er det som ligger i \(k_\infty\), altså en uendelig stor reaktor - for hvis reaktoren er uendelig stor vil jo heller ingenting noensinne kunne forsvinne ut av den. I vikeligheten er selvsagt ingen reaktor uendelig stor, og man må derfor også ta med at en viss del av nøytronene som produseres vil forsvinne.
Hvis sannsynligheten for at nøytronene skal bli i reaktoren er 0.7559 (det vil si 75.59%), eller, sagt på en annen måte 24.41% av alle nøytronene forsvinner ut av reaktoren, og da er de bare tapt :/ Når vi trekker fra de 24.41% som forsvinner, så sitter vi igjen med like mange nøytroner som vi startet med, og kjedereakjsonen er balansert og kritisk og veldig fin ♥
Bildet under viser nettopp forskjellen på en kritisk kjedereaksjon til høyre - altså at én fisjon i gjennomsnitt gir én ny fisjon, mens det er en overkritisk kjedereaksjon til venstre - altså at én fisjon gir feks tre nye fisjoner og hver av dem gir tre nye igjen...

PS: Et kjernekraftverk kan aldri eksplodere som en atombombe! Altså, den kjedereaksjonen som skjer i et kjernevåpen kan ikke skje i et kjernebrensel 🙂
PPS: Goood helg nydelige mennesker ♥♥♥
