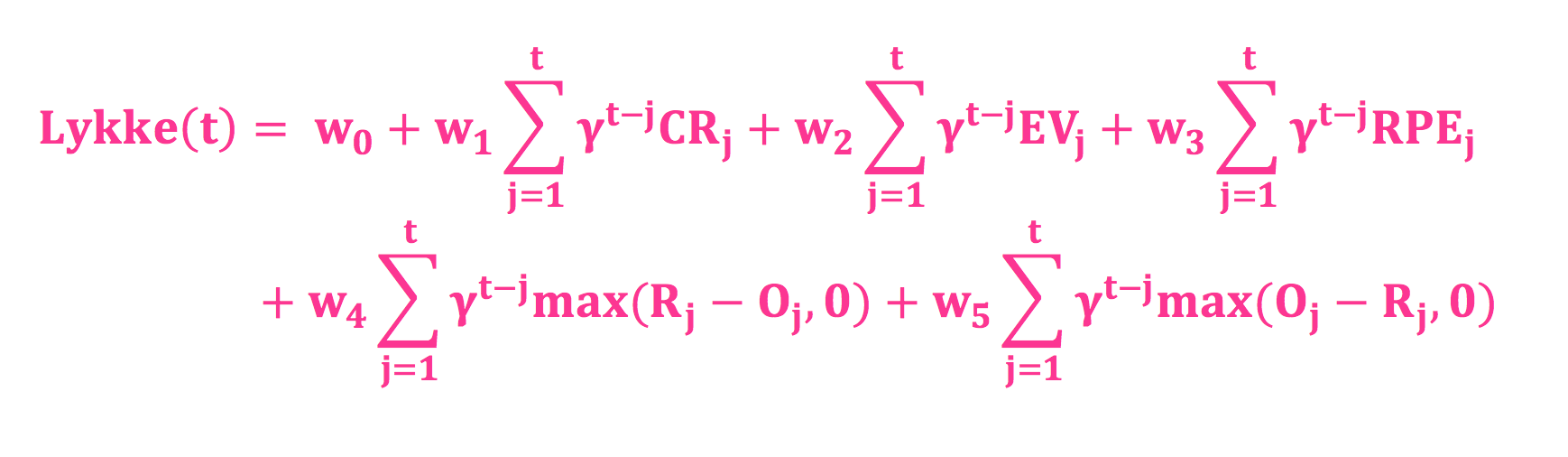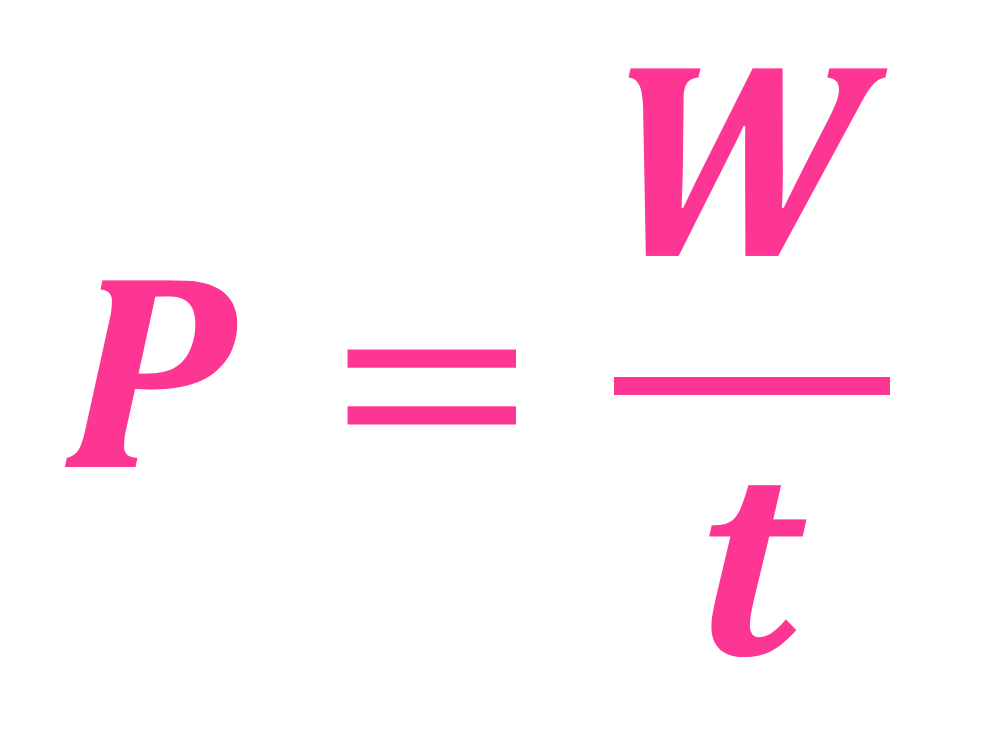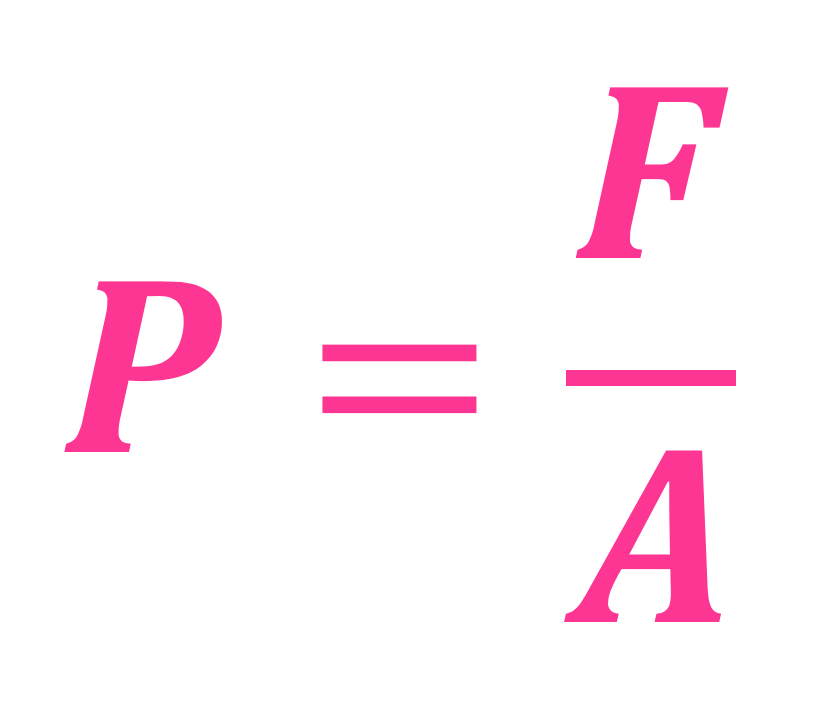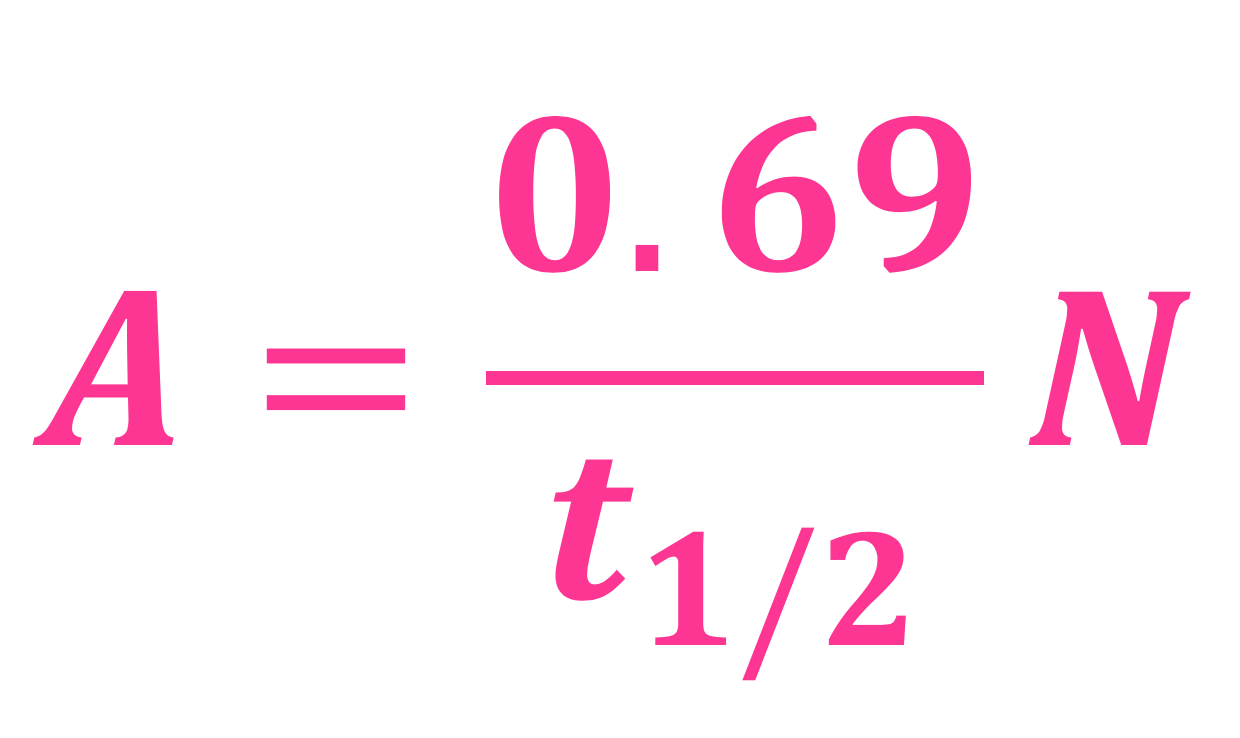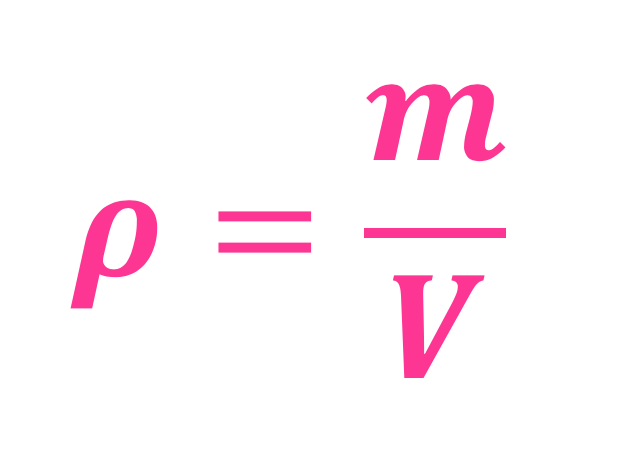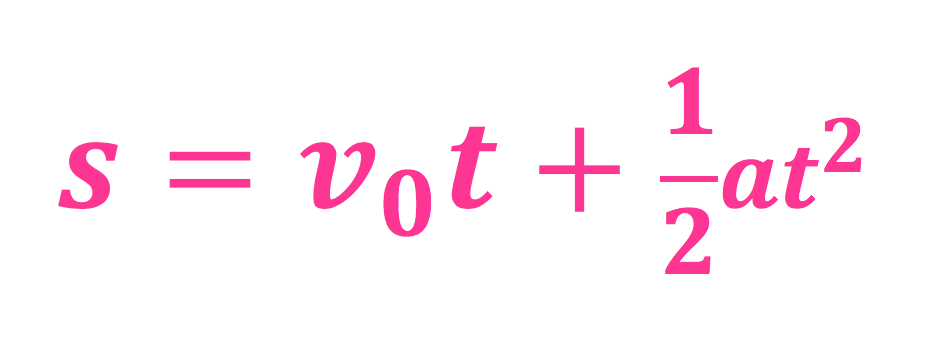Hei dere! Ukens formel er faktisk ikke ny, men jeg skal bruke den på et nytt spørsmål 😀 Sånn er det jo ofte i fysikken; formelen i seg selv er ikke nødvendigvis så avansert/vanskelig (noen ganger er den jo også det, men ofte er det to eller tre tall som skal ganges sammen, liksom - som man lærer å gjøre allerede i 2. klasse...), men det er det å bruke den riktig når det er noe i naturen du faktisk lurer på som er det som er vanskelig.
Spørsmålet det starter med er:
Har det noe å si om du lar kjøleskapsdøren stå åpen mens du feks heller juice i glasset, før du setter kartongen inn igjen og lukker døren, eller «må» du lukke døren mens du heller, for å spare energi (= penger)? Altså, bør du lukke døren mens du heller i glasset for å spare penger?
Får å kunne gi noe fornuftig svar på dette så trenger vi termofysikkformelen - den som handlet om spesifikk varmekapasitet. Den er veldig fin, og ser slik ut:

...og den er beskrevet og forklart HER 🙂
Når man skal svare på sånne spørsmål, så er det alltid lurt å først se på et «ekstremt» tilfelle – det er ofte lettere å sjekke hva skjer om all luften byttes i kjøleskapet byttes ut enn hva skjer om noe av luften i kjøleskapet byttes ut, feks: Så la oss se på det, da, at all luften inni kjøleskapet ble byttet ut med luft som har romtemperatur (som vi sier er 20 grader celsius). Hvor mye energi koster det å få all den luften ned til 4 grader igjen (som er temperaturen du ønsker i kjøleskapet)?
Den enkleste beregningen (og det er alltid lurt å starte med det enkleste - det enkel er ofte det beste, osv 😉 ), er faktisk å finne ut av hvor mye energi det koster å varme opp luften fra 4 til 20 grader, i stedet for det motsatte (som er å kjøle ned luften fra 20 til 4 grader): Da er det den fine formelen over som skal brukes. Siden spørsmålet er om energi, så er det Q som er den ukjente saken vi må finne ut av - da liker jeg best å stille opp formelen "riktig" før jeg skal begynne å gjøre noe med den. Da blir formelen som dette:
\(Q=m \cdot \Delta T \cdot c\)
Massen (vekten) til luften i kjøleskapet må vi regne ut, fra hvor mange liter det er i et kjøleskap: Et tomt kjøleskap har et volum på 240 liter (størrelse på et norsk, standard kjøleskap), som er det samme som 0.24 kubikkmeter (\(m^3\)). For å finne massen må man bruke massetetthetsformelen, som jeg har forklart HER. Massetettheten til luft er ca 1.225 kg/\(m^3\), og når du ganger dette med 0.24 finner du massen til luften i kjøleskapet, som blir 0.295 kg (luft veier ikke så mye 😉 ).
Det er altså (ca) 0.3 kg luft som skal kjøles fra 20 til 4 grader. \( \Delta T \) er temperaturforskjellen, altså 16 K, og m er 0.3 kg. Da er det bare c som mangler. c er den spesifikke varmekapasiteten til luft, som man må slå opp i en tabell (feks på wikipedia) for å finne; og den er 1.001 kJ/kgK.
Så er det rett og slett bare å sette sammen tallene, altså gange sammen massen og temperaturforskjellen og varmekapasiteten:
\(m \cdot \Delta T \cdot c = 0.294 \cdot 16 \cdot 1.001\) = 4.7 kJ (4700 Joule).
Dette betyr at for å varme opp luften trenger man 4.7 kJ energi – som er omtrent 0.001 kWh. I dag er prisen på én kWh ca 60 øre, og dermed koster det 0.06 øre å varme opp all denne luften – ca en tidels øre, da, for å få et tall som er hakket lettere (hvis strømprisen er 1 kroner per kWh så blir det også riktig med en tidels øre på den oppvarmingen av luften).
Så er det faktisk sånn at det å kjøle ned luft i et kjøleskap koster mindre energi enn det å varme den opp, så den tidelen av et øre er rett og slett en absolutt maks yttergrense av hva det koster å kjøle ned luften. Når du åpner opp kjøleskapsdøren i, la oss si, 30 sekunder, så kommer heller ikke all den kalde luften til å forsvinne ut – ikke i nærheten en gang.
Konklusjonen er at det å åpne kjøleskapsdøren, og la den stå åpen mens du gjør deg ferdig med å helle i juice eller melk eller vin eller hva nå enn det er du skal ha ut, koster «null».
(Hvis det er interesse for det kan jeg selvsagt gå mer i dybden på det med kjøling, og at det koster mindre å kjøle enn å varme opp – på en måte føler jeg det er litt sånn kontraintuitivt...vet ikke om det er sånn med dere også? Uansett: Rop ut hvis jeg skal ta mer om dette en annen gang 🙂 )
Forresten så har jeg kommet til en (foreløpig) løsning på kamerasituasjonen: Samme dagen som jeg la ut innlegget om at jeg er nødt til å skaffe meg et kamera, fikk jeg melding av Atle som sa at jeg kunne få låne (på helt ubestemt tid!) et kamera av han! På den måten kan jeg få prøve meg frem, og finne ut av hva som faktisk er viktig for meg, og hvor interessert jeg er i å lære. Kameraet jeg skal prøve å bli kjent med i sommer/fremover er et Sony RX 10.
Jeg er supertakknemmlig for at noen bare kommer og gir meg et sånt tilbud ♥ Så kan jeg avsløre at jeg allerede begynner å kjenne på at jeg nok kommer til å ønske meg et litt mindre kamera...eller at jeg får meg en skikkelig kul veske (jeg fant en jeg har lagt helt min elsk på) 😉

Ja, selfie er selvsagt det første jeg har prøvd meg på - men da har jeg i alle fall fått dokumentert første bilde tatt med annet kamera enn mobil. Så får vi jo se, da, om det blir noen utvikling...eller ikke.