Gooood søndag, håper helgen deres har vært like fin som min ♥ Vi tilbrakte en fantastisk, deilig, vårlig (nesten sommerlig?) lørdag i hovedstaden sammen med fine Katarina og Tom André. Det ble både drinker og bobler og Tjuvholmen og sol og måkeskrik - helt perfekt!

Vi MÅ jo bare ha en skikkelig bar/bartender i bryllupet vårt - cocktails er jo bare utrolig godt, og ikke minst kan de være utrolig vakre å se på.

---

Ukens formel er annengradslikningen - eller nærmere bestemt, hvordan man løser en annengradslikning 😀 Denne formelen har et eget navn; abc-formelen ♥

Oppskrift: abc-formelen

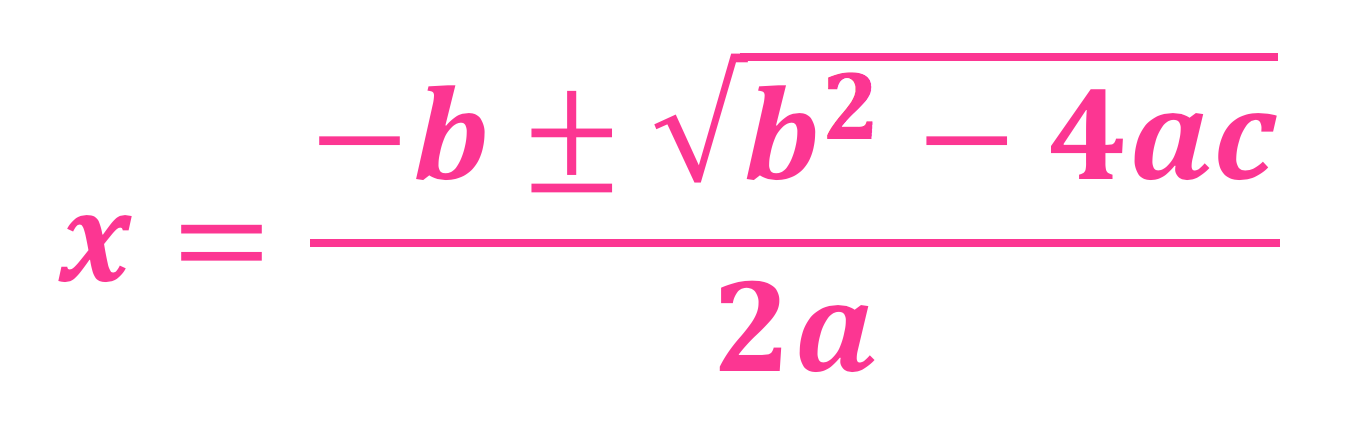
Hva det betyr

Kort fortalt så betyr formelen at hvis man har en annengrasdslikning så regner man ut x ved å sette inn riktige tall for a, b, og c. For å forklare hva dét igjen betyr - hvordan man gjør dette riktig - må vi først se på hvordan en annengradslikning faktisk ser ut. Generelt ser annengradslikninger slik ut:

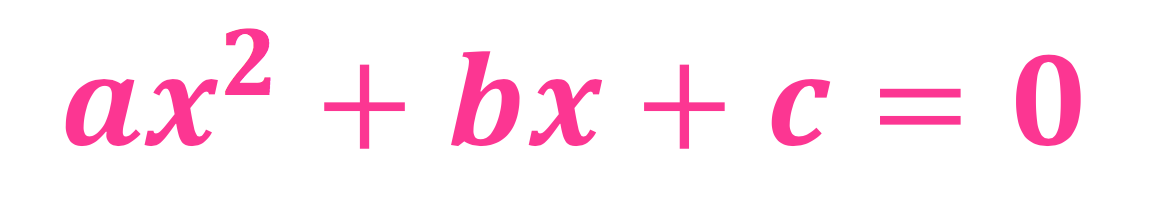
Det betyr at man har en likning som har ett ledd med \(x^2\), ett ledd med x, og ett ledd uten noen x - et såkalt konstantledd (konstant fordi det ikke forandrer seg selv om x forandrer seg 😉 ). Det tallet som står foran \(x^2\) er a, det tallet som står foran x er b, og det leddet som bare er et tall, uten noen x, er c.

Fremgangsmåte

Antageligvis så er det lettest å forstå hvordan man bruker abc-formelen med et eksempel. Hvis vi har annengradslikningen \(x^2+4x+4=0\)

For å finne a, b, og c så er det superviktig at man "rydder opp" slik at likningen blir stående riktig (og ryddig - ryddig er bra!); det vil si at alle \(x^2\) samles sammen, alle x samles sammen, og at det står 0 på høyre siden av er lik-tegnet. Likningen over her er allerede ferdigryddet, og a = 1, b = 4, og c = 4. Så er det bare å sette tallene inn i abc-formelen:

\(x=\frac{-4\pm\sqrt{4^2 - 4\cdot1\cdot 4}}{2\cdot 1}\),  som blir   \(x=\frac{-4\pm\sqrt{16 - 16}}{2}\),   og videre  \(x=\frac{-4\pm 0}{2} = \frac{-4}{2} = -2\).

Løsningen på \(x^2+4x+4=0\) er at x = -2, og det finner vi med abc-formelen.

---

Når jeg sier at det er viktig å "rydde opp" først så mener jeg at hvis likningen vår sto som dette: \(2x^2+x=x^2-3x-4\) så må den ryddes opp i før vi kan finne a, b, og c, på denne måten \(2x^2-x^2+x+3x+4=0\), som blir den samme likningen som over, altså  \(x^2+4x+4=0\). Vanligvis så er det to løsninger for annengradslikninger, altså at x er enten dette eller dette, liksom, men akkurat dette eksempelet er et spesialtilfelle der det bare fins én løsning 🙂

Det går helt fint at både b og c er 0, men a, må være et annet tall enn null (det kan godt være negativt, bare ikke akkurat null) - hvis ikke så fins det ingen \(x^2\), og da er det liksom ingen annengradslikning lenger 😉 Bortsett fra akkurat det at a må være noe annet enn akkurat null så kan a, b og c være hva som helst 😀

---

Annengradslikninger kommer man til ca hele tiden innen f.eks. geometri eller fysikk (eller kombinasjonen - det er en god del geometri i fysikk). Ett eksempel fra fysikk er hvis man kaster en ball (eller en sko, eller en veske, eller laptopen fordi du er sint, hva nå enn), så trenger man abc-formelen for å finne ut hvor lang tid det tar før det du kaster treffer bakken. (Eller hvor lang tid det tar før det har falt halvveis ned til bakken eller hva 😉 )

Kanskje akkurat dette med skrått kast passer til neste Formelfredag...? 😉

 

 

 

 

Endeldig Formelfredag igjen! Denne gangen blir det en klassiker, som kanskje passer ekstra bra for alle som har gått opp og ned fjelltopper i løpet av påsken? Vi går rett på sak; denne uken får dere oppskriften på en rett linje 😀

Oppskrift

Hva det betyr

y er navnet på linjen, eller grafen (du kan velge helt selv om du syns det passer best å kalle det linje, eller graf 😀 ).

På høyre side av er lik-tegnet kommer selve beskrivelsen, eller oppskriften, på y - altså grafen. Først står det ax, som betyr a ganget med x. a kalles for stigningstallet i denne likningen, og forteller hvor bratt kurven kommer til å bli. Hvis a er 1 så betyr det at hvis du går 1 til siden på x-aksen i et koordinatsystem (feks fra 1 til 2), så går du 1 opp på y-aksen (i det samme koordinatsystemet 😉 ). Hvis a er 0.5 så betyr det at når du går 1 til siden på x-aksen, så går du bare en halv (0.5) oppover på y-aksen. Hvis a er minus 2, så betyr det at når du går én til siden på x-aksen så går du ned 2 på y-aksen; når det er minustall foran a så går grafen nedover, og når det ikke er noe minustall så betyr det at grafen går oppover. Jo større a er (enten positivt eller negativt - hvis du skal være pirkete på det, så, ja, jeg mener absoluttverdien av a 😉 ), desto brattere blir grafen - enten oppover eller nedover.

x er x - verdien på x-aksen i koordinatsystemet der denne grafen skal plottes 🙂

b er konstantleddet. Det heter det fordi det er konstant - altså det samme hele tiden. Dette tallet (det skal jo være et tall 😉 ) forteller hvor grafen/linjen krysser y-aksen: Hvis b er 3, så betyr det at linjen krysser y-aksen i 3, hvis b er minus 2, så krysser det i minus 2, osv...

a og b er bare ganske vanlige navn å gi til stigningstallet og konstantleddet. Hvis jeg skriver y = stigningstall*x+konstantledd så er det akkurat den samme oppskriften som over, bare med andre navn (litt mer klønete, men kanskje mer besrkivende) for stigningstall og konstantledd. Jeg kunne også ha skrevet oppskriften sånn: y = flippetiflopp*x + TanteAgata (enda litt mer klønete, og absolutt ikke besrkivende - men allikevel betyr det det samme - det syns jeg er gøy, flippetiflopp er blitt min favorittvariabelnavn 😀 )

 

Fremgangsmåte

For å plotte dette som en rett linje (som jeg påstår at dette blir), så må vi jo ha noen punkter å plotte i koordinatsystemet. Hvis vi har at a=-2 og b=3 så ser formelen slik ut: y = -2x + 3, og da kan vi begynne å finne koordinatene slik at vi kan lage plott - og se at det faktisk blir en rett linje 🙂

Man starter med å velge forskjellige verdier (tall) for x, og ut fra det kan man regne ut hva y blir:

• x = 0; da blir y = -2*0 + 3 = 3
• x = 1; da blir y = -2*1 + 3 = 1
• x = 4; da blir y = -2*4 + 3 = -5
• x = 10; da blir y = -2*10 + 3 = -17

Når dette plottes i et vanlig x-y-kooordinatsystem ser det sånn ut - som jeg sa så går linjen nedover når stigningstallet er negativt, og det er jo ganske tydelig 😀

Nå har jeg med vilje bare plottet akkurat det fire punktene jeg regnet ut over, men man ser jo ganske tydelig at dette er en rett linje...hvis du er i tvil så kan du jo prøve velge flere forskjellige verider for x, som ligger fe mellom 4 og 10, og se at de verdiene du får for y da kommer til på lande nøyaktig på den rette linjen mellom de to punktene lengst mot høyre.

---

Denne uken har jeg også lyst til å vise hvordan man kan gjøre hvis du vil plotte dette i Python - altså skrive en bitteliten kode som gjør at du kan plotte en rett linje:

Dette ser ut sånn når programmet kjører:

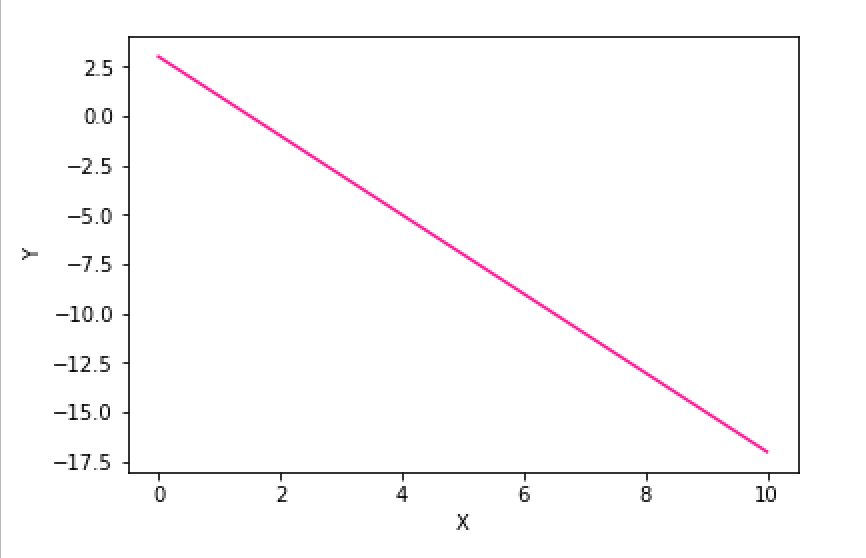Her er det altså regnet ut hva y blir for 100 punkter fra x er 0 til x er 10, og så er det trukket en rett strek mellom hvert av disse punktene - og man ser at y = -2*x + 3 er en rett linje. Jeg har selvsagt valgt å plotte denne i fargen "deeppink", for det liker jeg å gjøre ♥

Hvis a er 2 i stdete for -s blir hele likningen: y = 2*x + 3, og da ser det slik ut (for at det ikke skal være det samme har jeg valgt å plotte i "cyan"):

Hvis a er 10 og b er -5 blir hele formelen y = 10*x -5, og det ser slik ut (fargen er "springgreen"):

Her kan man lure seg litt til å tro at dette bare ser helt likt ut som det forrige plottet, og at det ikke er noen forskjell om stigningstallet var 2 eller 10, og at jeg bare har løyet...men hvis man ser på tallene på y-aksen ser man at disse er forskjellige på de to siste plottene - det siste med stigningstallet lik 10 (grønn farge) går jo MYE høyere opp enn det med stigningstall lik 2! Hvis jeg plotter dem sammen ser man det godt - det er viktig (og lurt!) å ikke la seg lure ♥

...

Jeg går forresten selvsagt ikke rundt og husker på hva de forskjellige fargene heter, men Google er virkelig min venn når det kommer til å programmere. Denne gangen søkte jeg bare på pink python plot, og da fant jeg raskt dette bildet:

---

Håper alle fine lesere har hatt en fin helg, selv om det fine været på fredag (altså, elsk ♥) ikke holdt seg - på den positive siden så tar jo regnet med seg mye av den resterende snøen. Her skal det spises burgere nå, mens vi ser en episode Weeds, deretter håper jeg vi klarer å komme oss litt tidlig i seng. Hele april er crazy med ting som skjer, så vi må komme oss opp tiiidlig i morgen - OG være skikkelig uthvilte (funker dårlig å komme seg opp tidlig hvor hodet ikke er skikkelig med, da blir det jo ingen effektiv dag).

Husk at det er lov å komme med ønsker til formelfredag, da, dere! Jeg har fått noen tidligere (feks E=mc2), og jeg trooor jeg har tatt alle som har blitt etterspurt... Vi snakkes ♥

Hei lillelørdag!

Her kommer en slags oppfølging til forrige ukes Formelfredag, som jo handlet om Pytagoras – som sier at \(katet^2 + katet^2 = hypotenus^2\). Jeg kommer tilbake til dette med Pytagoras lenger ned i dette innlegget, men først må jeg bare gi dere oppskriften på arealet av et kvadrat:

 

Oppskrift

 

Hva det betyr

Et kvadrat er en firkant der alle sidene er like lange. Jeg kaller sidene for "s" i figuren under (hvis de ikke var like lange kunne jeg ikke kalt begge for "s" 😉 ). Arealet av en hvilken som helst firkant er lengde ganget med bredde, men i spesialtilfellet kvadrat så er jo lengden og bredden akkurat like lange, og dermed blir det s ganget med s som er det samme som \(s^2\).

A står for areal 🙂

Fremgangsmåte

Dette er jo en veldig enkel formel, og fremgangsmåten blir tilsvarende lett: Hvis s = 5 så blir arealet \(5 \cdot 5=25\).

Hva det betyr 2:

Grunnen til at jeg kaller dette en oppfølging av Pytagoras-innlegget er selvsagt fordi at når vi slår sammen Pytagoras og arealet for et kvadrat så står det faktisk at hvis vi lager kvadrater av alle sidene i en (rettvinklet) trekant, så er det sånn at arealet av de to korteste sidene i trekanten (katetene) blir nøyaktig like stort som arealet av kvadratet på hypotenusen (den lange siden). Pew, lang setning...

Og det ser sånn ut:

For å gjenta: Arealet av de to minste kvadratene i figuren over blir akkurat det samme som arealet av det størset kavdratet. Jeg syns det er helt sinnsykt fascinerende at det er sånn!

 

---

Nå skal jeg en tur ut med jentene - vi pleier å møtes på Mat og Mer, og det er litt ekstra stas igjen nå som ingen er gravide, og alle kan spise spekepølse og ta seg et glass vin (plis ikke skyt meg for å si at det er hyggelig at alle kan drikke – vær gjerne uenig, men sånn er nå min mening). Koselig blir det garantert, uansett! Vi snakkes ♥

Søndag kveld allerede? Det har gått ganske i 100 denne helgen; vi har hatt både Andrea og Arian (fien niese og nevø) på overnatting, og de dro for ikke aå alt for lenge siden. Veldig veldig hyggelig, men tiden går jo, og det blir litt ekstra opprydding... Uansett, nå får det holde med Formelfredag-tørke, og jeg er heldigvis godt innafor med Formelfredag/ukens formel nå - det er tross alt nesten tre timer til klokken vipper midnatt, og det offisielt er en ny uke 🙂

Ukens formel er en VIRKELIG klassiker, nemlig Pytagoras' formel, og jeg syns rett og slett vi bare bretter opp ermene, og går rett på sak:

 

Oppskrift

Hva det betyr

For å forklare hva denne oppskriften faktisk betyr trenger vi å se på trekanten under:

Det som er spesielt med denne trekanten er at den er en såkalt rettvinklet trekant, som betyr at den ene vinkelen (den nede, i venstre hjørne) er rett. At en vinkel er rett betyr at den er 90 grader, og man markerer at en vinkel er akkurat 90 grader med å tegne et sånt hjørne over den, som jeg har gjort 😉 Pytagoras handler om sånne, rettvinklede trekanter.

Denne trekanten har, som alle trekanter (rettvinklede, og andre), tre vinkler; altså to i tillegg til den rette vinkelen. I figuren min har jeg markert en av de to andre vinklene - den nede i høyre hjørne. Jeg har gitt den det flotte navnet "V" (jeg kunne ha kalt den, feks, "flippetiflopp", men det er mer vanlig å kalle vinkler for "V" - det er også enklere og raskere å skrive). Men poenget i selve Pytagoras-oppskriften er ikke disse vinklene; det er de tre sidene er det som er viktig. Vi trenger dog å markere vinklene for å vite hvilke av de tre sidene det er vi snakker om...

Den lengste siden i trekanten, som går fra "V" og til den siste vinkelen, som jeg ikke har snakket om, og som er navnløs, heter "Hypotenus". De to andre sidene heter "Katet", men som du kan se på figuren min så heter den ene "Hosliggende katet" og den andre "Motstående katet". Det med hosliggende og motstående har å gjøre med "V". Den som er "hosliggende" er ved (hos) den vinkelen som heter "V", og den som er "motstående" står altså "mot" "V".

Det med at den ene kateten heter hosliggende, og den andre heter motstående er egentlig ikke viktig akkurat nå med pytagoras; men det kommer til å bli viktig neste uke, og derfor tenkte jeg det var like greit å bare ta det nå med én gang - litt rettvinklede treknater-lærdom der, altså ♥

\(katet^2\) betyr katet ganget med katet (altså at kateten skal ganges med seg selv), og \(hypotenus^2\) betyr hypotenus ganget med hypotenus (hypotenus ganget med seg selv). Først tar man den ene kateten og ganger med seg selv, så tar man den andre katenten og ganger med seg selv, og dett er altså det samme som hypotenusen ganget med seg selv (hvis noen lurer på hvorfor jeg ikke sier noe om areal, så er det med vilje, og det kommer en annen dag, og hvis du ikke tenkte på areal i det hele tatt så kan du bare se bort fra denne parentesen 😉 ).

Fremgangsmåte

Så lenge vi vet hvor lang to av sidene i en (rettvinklet) trekant er, så kan vi regne ut hvor lang den siste siden er med Pytagoras.

Hvis feks den ene kateten er 5 cm, og den andre kateten er 3 cm, så blir hypotenusen:

\(5\cdot5+3\cdot3=hypotenus^2\), og videre blir det  \(25+9=hypotenus^2=26\)

Siden \(hypotenus^2\) er 26, så blir hypotenusen hvadratroten av 26: \(\sqrt{26}\)=5.099. Hvis du ikke har en kalkulator som kan regne ut kavdratroten av et tall så har du faktisk det allikevel, det er bare å skrive sqrt(26) i søkefeltet i nettelseren 😀

Hvis vi vet hvor lang den ene kateten er, og hypotenusen, kan du finne den siste kateten. Hvis feks hyptenusen er 7 cm, og den hosliggende kateten er 6, så blir den motstående kateten:

\(6\cdot6+katet^2=7\cdot7\), og videre blir det  \(36+katet^2=49\). Så flytter vi 36 over til høyre siden av er lik-tegnet, slik at den kateten vi ikke vet lengden på blir stående alene: \(katet^2=49-36=13\). Da vet vi at den ukjente kateten (i dette tilfellet den motstående kateten) ganget med seg selv blir 13, og for å finne hvor lang den faktisk er så tar vi kvadratroten av 13: \(katet=\sqrt{13}=3.606\)

...og selvfølgelig brukes Pytagoras til masse, men det må bli en annen gang. I kveld holdert vi oss toil å bare se på hvordan formelen faktisk er, og hvordan man bruker den.

---

Bonus: Andy the Candy har en veldig fin (syns Anders og jeg, i alle fall) sang om Pytagoras. Hør den her ♥♥♥

 

 

Hei fredag 🙂 Eeeh...lørdag!

Ja, jeg innrømmer lett at jeg ser på The big bang theory, og jeg elsker det! Jeg følte meg omtrent nøyaktig som Penny de første årene av studiene mine, på så mange måter. Til slutt så ble jeg jo jammen sammen med nerden også - så skal det sies at jeg i aller høyeste grad også er nerd, bare kanskje ikke helt prototypen 😉

Uansett, på mandag satte jeg på TVen i bakgrunnen, og hadde på random lineær-TV for første gang på 4(?) år, og da var det TBBT som gikk. I episoden var Leonard, Raj, og Howard på telttur, og ut på kvelden sier Leonard at han blir svimmel fordi han plutselig kjenner hvor fort jorden beveger seg (de har vel ved et uhell fått i seg noe de ikke egentlig skulle ha fått i seg før dette skjer ). Denne scenene ga meg ideen til Formelfredag denne uken: Ukens formel er omkretsen av en sirkel - det virker kanskje ikke som tidenes mest sexy formel (borsett fra at sirkel er en veldig perfekt og egentlig ganske sexy form), men jeg vil bruke den til å regne ut nettopp hvor fort vi/jorden beveger oss, og det er jo ganske gøy 🙂

 

 

oppskrift

 

hva det betyr

O er omkrets – altså lengden rundt, i dette tilfellet en sirkel. \(\pi\) er \(\pi\) – ofte sier vi det er 3.14, men \(\pi\) er et irrasjonalt tall; som har uendelig med desimaler (som ikke har noe mønster - det betyr blant annet at absolutt alle vil finne sin egen fødselsdato i desimalene til \(\pi\)), så 3.14, eller evt 3.1415 er bare en forkortelse. r er radius, altså lengden fra midten (sentrum) av en sirkel og ut til kanten.

 

fremgangsmåte

Hvis radius på en sirkel er 6378 km blir omkretsen av denne sirkelen: \(2 \cdot3.1415\cdot6378\) = 40 074 km = 40 074 000 m.

Dette er omkretsen rundt ekvator. Og dette er den lengden man beveger seg rundt på ett døgn (hvis man er ved ekvator).

Da kan vi bruke s=vt til å finne ut hvor fort man beveger seg. Vi vet at s =40 074 000 m (omkretsen rundt ekvator), og t = 24 timer = \(60\cdot60\cdot24\)=86400 sekunder er ett døgn, altså den tiden man bruker på å komme seg rundt. Da blir farten, \(v = s/t = 40074000/86400\) = 463 m/s.

Dette betyr altså at hvert eneste sekund beveger man seg 463 meter!

Her oppe i Oslo, går det ikke like fort: Vi bruker jo også et døgn på å komme oss rundt, men siden vi er nærmere Nordpolen så er det kortere vei for oss å komme rundt. Radius på vår sirkel (60 breddegrader) er 3189 km, og omkretsen "vår" blir dermed \(2 \cdot3.1415\cdot3189\) = 20 037 = 20 037 000 m. Farten vi fyker avgårde med blir  \(v = s/t = 20037000/86400\) = 232 m/s. Vi beveger oss altså ganske fort her oppe i nord også: På den tiden det tar å trykke publiser på dette innlegget så fyker jeg mer enn 200 meter avgårde.

Man kan jo skjønne at Leonard føler seg litt svimmel 😉

 

 

 

 

 

Nå er 2018 kommet godt i gang, og med den (arbeids)uken som nå er over føler jeg tempoet har blitt skrudd opp til vanlig igjen. Da er det selvsagt helt på sin plass at Formelfredag kommer tilbake fra ferie (eller hva nå enn jeg skal kalle pausen 😉 ).

Jeg syns at dette året må starte med en kjendis, og hvilken likninger er vel mer kjent enn Einsteins formel for masseenergi...? Jeg kommer ikke på noen annen likning som er mer kjent, i alle fall. Kaaanskje like kjent, men ikke mer - hva tenker du?

---

oppskrift

 

hva det betyr

Denne likningne er egentlig ganske enkel på formen sin, og med ord står det at energi er lik masse ("vekt") ganget med lysets hastighet (fart) i annen. Dette er den energien som faktisk ligger i massen til noe, og med andre ord kan man si at masse er energi og energi er masse. Masse kan bli til annen energi (dette skjer i en atombombe), og energi kan bli til masse (dette skjer når man på CERN lager større og tyngre partikler - sånn som feks Higgs-partikkelen, som man laget/oppdaget for første gang i 2012).

 

fremgangsmåte

I likningen/oppskriften står det altså at energi (E) er lik masse (m) ganget med lysets hastighet ganget med lysets hastighet (\(c^2\)). Lyset går veldig fort, faktisk går det 300 000 000 meter per sekund. Det er ingenting som kan gå raskere enn lyset. (Ok, alle flisespikkere der ute; dere har helt rett i at 300 000 000 er en tilnærming, og at hastigheten er rett under denne verdien. For alle praktiske formål så stemmer den farten jeg har satt 😉 )

Hvis m = 75 kg så blir energien altså \(75 \cdot 300 000 000 \cdot 300 000 000 = 6750000000000000000 J\), eller 6.75 exajoule - dette er SYKT mye energi! Sagt med litt andre ord: Det er nesten like mye som det hele EU bruker av elektrisk energi på ett  år. I én voksen person, altså.

Vanligvis så er det atomkjerner og sånn man bruker denne formelen for, spesielt med det jeg har jobbet med de siste årene - fisjon. Når en tung kjerne (feks uran) fisjonerer så er det faktisk sånn at de to fisjonsproduktene, eller spaltingsproduktene, som er det uranet blir til etter på ha delt seg, veier mindre etter delingen, enn før. Det vil si at hvis du tar vekten til hver av de to spaltingsproduktene (pluss eventuelle nøytroner som falt av i det kjernen delte seg), og ser hva alt dette veier til sammen, så veier det MINDRE enn det urankjernen gjorde først. Det er nettopp fordi bittelitt av massen til uranet har blitt til energi 🙂 Dette er stikk motsatt av hvordan det er med feks et tårn av legoklosser (hvis du sammenlikner et legotårn med urankjernen); da har det ingenting å si om du veier 10 legoklosser som er satt sammen, eller om du tar å deler legotårnet i to, og veier de to småtårnene hver for seg og så legger sammen. Hvis hver legokloss veier 10 gram, så kommer de 10 klossenen til å veie 100 gram uansett om du setter sammen 5 og 5, eller alle 10 sammen 🙂 Sånn er det altså ikke når du begynner å dele opp atomkjerner.

Håper dette var forståelig på en søndags kveld ♥

---

 

Bildet under er fra fredag morgen, mens jeg satt og ventet utenfor studio, før jeg skulle snakke med en ekte kreasjonist på P1 (jorden er 6000 år gammel type kreasjonist). Veldig usikker på om det egentlgi hadde noe som helst for seg...jeg syns i alle fall det egentlig ble ganske ubehagelig :/ På bildet under aner jeg stort sett fred og ingen, og er ganske fornøyd, da, men jeg var ikke så veldig fornøyd etterpå, dessverre.