Hei Formelfredag nummer 9! Endelig har jeg kommet dit at den aller mest naturlige likningen var en av bevegelseslikningene, og jeg ser ingen grunn til å vente lenger nå, så da tar vi på oss likningsøynene og setter i gang:
- oppskrift -
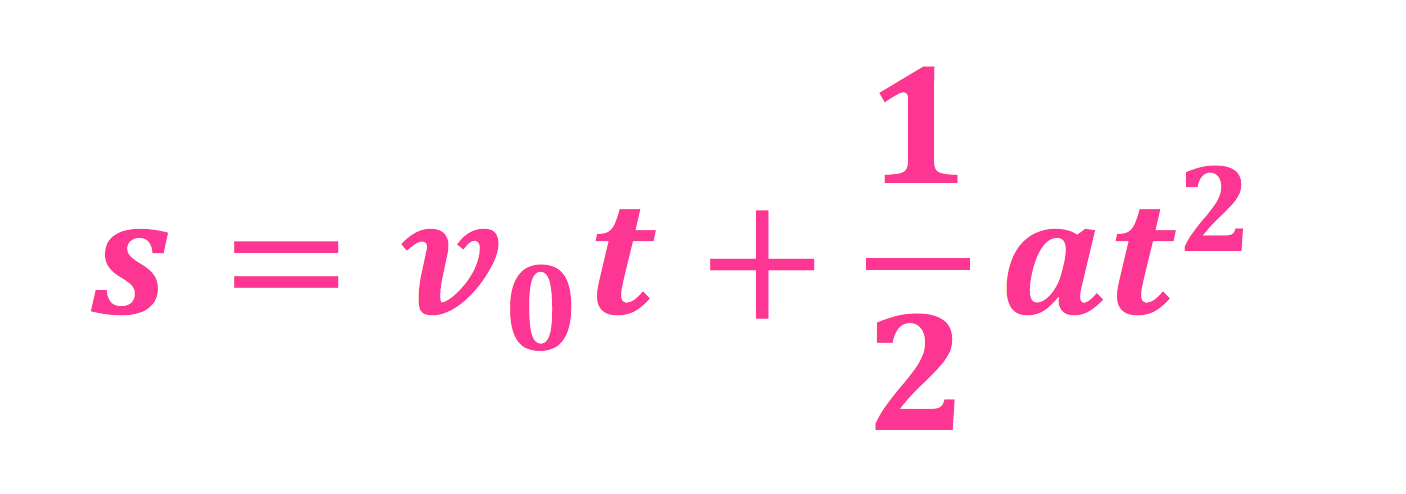
- hva det betyr -
For en stund tilbake handlet ukens formel om den søte klassikeren, strekning, fart og tid, som alle har lært en eller annen gang på skolen. Den ser jo slik ut: s = vt, så hvorfor da enda en formel for strekning, fart og tid - som er det også denne Formelfredagen handler om...?
Vel, som dere ser så er det ikke bare s og v og t i denne formelen, men også a. Så den enkle formelen (s = vt) kan du bruke for å finne ut hvor langt du kommer når farten din er den samme hele tiden, mens denne formelen kan du bruke for å finne ut hvor langt du kommer etter en viss tid når farten din forandrer seg – altså at du akselerer. MEN: vikitg, viktig, viktig! I denne formelen så kan ikke akselereasjonen forandre seg, den må altså være konstant.
s = strekning (i meter), 1/2 er en halv, \(v_0\) = farten du starter med (i m/s), 0 her betyr nettopp det - rett før du begynner å aksellere (dette er en veldig vanlig måte å markere at man snakker om noe som skjer akkurat i det man begynner å måle, feks), t = tid (i sekunder), a = akselerasjon (i \(m/s^2\)), og \( t^2 \) er tid (i sekunder) ganget med tid (i sekunder).
- fremgangsmåte -
Sånn som formelen står nå så regner man jo ut hvor langt man kommer hvis man har en eller annen startfart, og så akselerer du i en eller annen tid, men den kan jo selvsagt løses på alle mulige andre måter også 🙂 Jeg vil gjerne bruke den nå til å følge opp forrige ukes Formelfredag, der det var snakk om å falle ned 40 meter. Da kan vi nemlig bruke denne formelen til å finne ut hvor lang tid det tar før man treffer bakken. Hvis man står i 14. etasje, 40 meter over bakken, og faller så blir det slik:
- s = 40 m
- \(v_0\) = 0 m/s (før du faller så er farten din null, i fallretningen)
- t er den vi ikke vet noe om
- a = 9.81 \(m/s^2\) - akselerasjohnen når man er i fritt fall er altså rett og slett tyngdeakselerasjonen, som man også kaller for g 🙂
Siden startfarten (\(v_0\)) er null så blir det litt enklere å løse likningen, for da blir det første leddet, \(v_0 \cdot t\), bare null - for når noe ganges med null så blir det null. Sånn er dét, liksom 😉 Så da blir det seende slik ut \( s = 1/2at^2 \) (løsningen for 2.gradslikning bør kanskje være neste ukes formel, for den trenger man jo hvis man skal løse denne med tid, og farten til å begynne med ikke er null...?). Så setter man inn tallene, og da blir det sånn:
\( 40 m = 1/2 \cdot 9.81 m/s^2 \cdot t^2 \), og når tall som kan ganges sammen ganges sammen blir det \( 40 m =4.905 m/s^2 \cdot t^2\). Nå har vi en liten, søt likning der vi kan finne først \(t^2\), og så t:
\((40 m)/(4.905 m/s^2) =t^2 \)Så er det kvadratroten på begge sider av er lik-tegnet, og da står man igjen med t, som jo er akkurat det man vil - siden \(t^2\) ikke gir så mye mening sånn i hverdagen, men t, altså tid, gir ganske mye mening 😀
\(t = \sqrt {40/4.905}\) = 2.86 sekunder.
Så: Hvis man slipper ned noe (eller er så utrolig uheldig at man faller ned selv) fra 14 etasje (40 meter over bakken), så tar det litt under 3 sekunder før det treffer bakken. Det er mulig jeg er litt rar, men jeg elsker å regne på sånne ting: hva blir farten, hvor lang tid tar det, hva slags energi er det snakk om, osv 😀
Ellers håper jeg alle nyter fredagsroen! Selv så savner jeg Anders veldig, men jeg har fått meg et glass (nei, jeg bare tuller; jeg har fått 2.5 glass, snart 3) vin, og nå er det heldigvis ikke lenge til han kommer hjem igjen - og da skal han i alle fall ikke reise mer til USA før det ståe 2018 i kalenderen ♥
PS: Dette er en sånn formel der man kan se ganske lett, egentlig, selv at det blir riktig når du setter inn de forskjellige enhetene - i alle fall når man har treningen på det 🙂
PPS: Svaret på forrige ukes spørsål til dere, fine lesere, kommer i et eget innlegg – og da kan det jo hende at det kommer en liten ny utfordring til dere, med denne formelen.
