Hei fredag, og hei igjen fredagsspalten (som har hatt veeeldig lang ferie nĂ„ đ ), nemlig Ukens Formel â„ Sist gang jeg presenterte ukens formel handlet det om halveringstid som forklarer hvordan man finner ut hvor mye Uran (eller andre radioaktive stoffer) man sitter igjen med hvis man starter med for eksempel 1 tonn og venter 4.5 milliarder Ă„r (dette er jo nesten jordens alder).
Denne gangen skal vi snakke om sĂžsteren til halveringstidsformelen, nemlig formelen for eksponensiell vekst. At noe vokser eksponensielt betyr at hvor mye det vokser med er en prosentandel av hvor mye du har. Dette kjenner vi godt igjen fra nĂ„r man bruker kredittkort og ikke betaler. Et typisk kredittkort har rente pĂ„ omtrent 20% i Ă„ret. Dette betyr at hvis du lĂ„ner 10000 kroner og ikke betaler tilbake, skylder du 2000 kroner ekstra det neste Ă„ret (veksten er 2000 kroner), og lĂ„ner du 100000 kroner vokser gjelden med 20000 kroner. Veksten er altsĂ„ avhengig av hvor mye du har (det er det som menes med at den vokser proporsjonalt đ )!
Halveringstidsformelen er egentlig bare en spesialversjon av den mer generelle formelen for eksponensiell utvikling. Den ser slik ut:
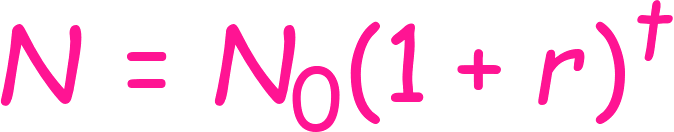PÄ samme mÄte som i formelen for halveringstid er
- N0Â hvor mye du starter med (for eksempel 10000 kroner)
- r er vekstraten (renten)
- t er hvor lang tid det gÄr (ofte antall Är)
- N er hvor mye du har til slutt
Siden renten fra kredittkortselskapet ofte er i prosent mÄ vi dele det tallet pÄ 100 for Ä sette inn i formelen (20% er 0.20), og altsÄ fÄ vekstraten. SÄ for Ä ta eksempelet over med 100000 kroner:
\(N = 100000\cdot(1+0.20)^1 = 100000\cdot 1.20^1 = 120000\), altsÄ 20000 kroner mer enn vi startet med. Vi kan nÄ finne ut hvor mye vi skylder etter 10 Är ved Ä sette inn 10 i stedet for 1, og da betyr det at man mÄ ta det tallet som vi fÄr inni parentesen (i dette tilfellet sÄ er det 1.20) og gange med seg selv 10 ganger:
\(N = 100000\cdot(1+0.20)^{10} = 100000\cdot 1.20^{10} = 100000\cdot 6.19 = 619173\), over en halv million mer enn det vi lĂ„nte. SĂ„ med eksponensiell vekst sĂ„ gĂ„r det liksom fortere og fortere, og det er litt kjedelig med renter nĂ„r du skylder mye penger - i alle fall hvis renten er hĂžy, sĂ„nn som med kredittkort đ
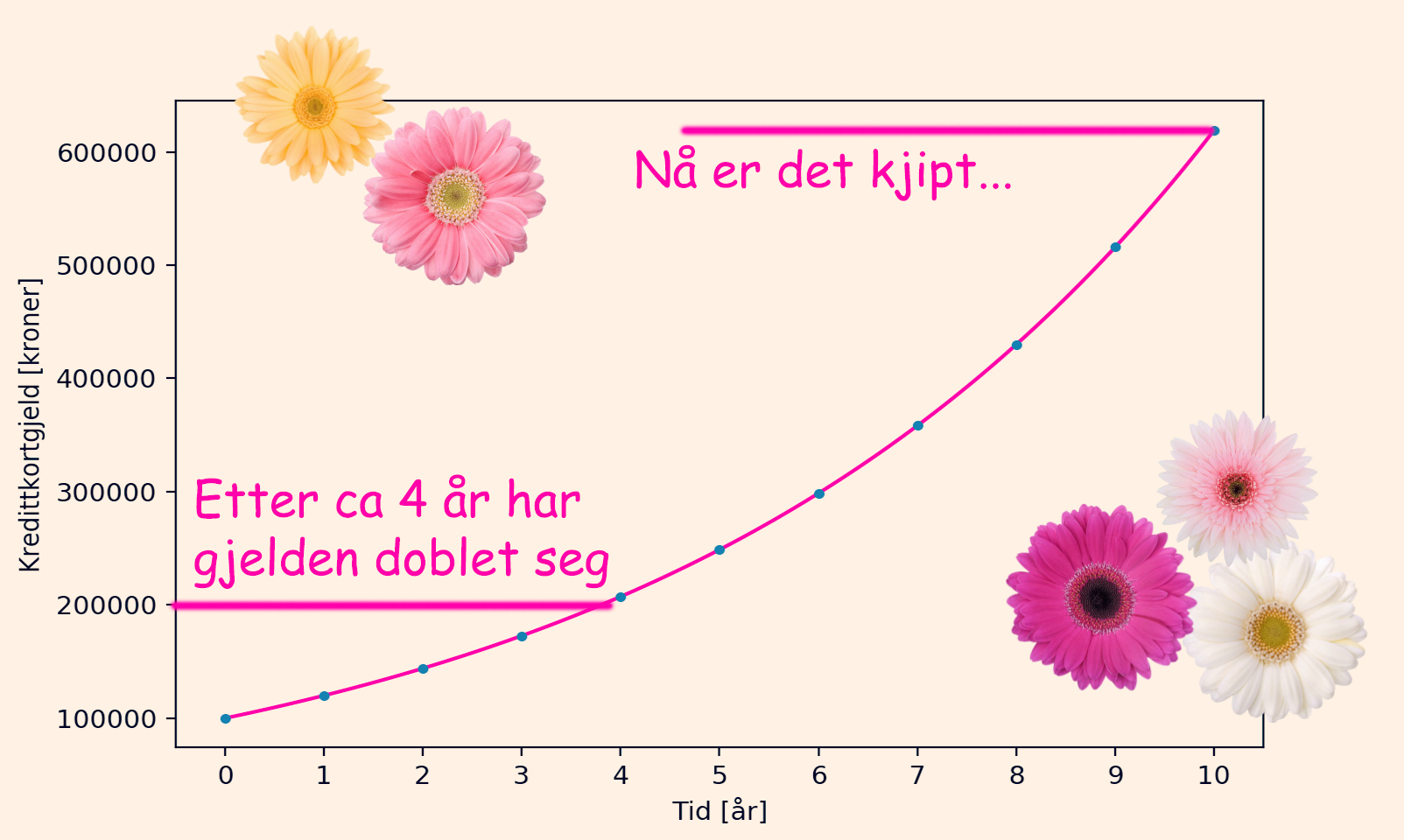
Denne formelen blir brukt overalt hvor vekstraten er proposjonal med hvor mye du begynner med. I biologi (og medisin sÄ klart) ser man ofte pÄ bakterievekst eller andre mikroorganismer der vi ser eksponensiell vekst. I USA ser det ut til at befolkningen over de siste 100 Ärene er godt beskrevet av eksponensiell vekst med 1.5% vekstrate.
PS: noen reagerer kanskje pĂ„ at formelen er i den flotte(?) fonten "comic sans"... Vel, denne fonten er faktisk ganske mye brukt blant fysikere rundt omkring i verden, blant annet av fantastiske Fabiola da hun annonserte at de hadde funnet Higgs pĂ„ CERN. Hvis fonten er bra nok for Fabiola, er det bra nok for meg â„
Fun fact: Da Alan Turing fant opp LaTeX pÄ CERN i 1991, ville han fÞrst ha Comic Sans som standardfont, ikke Computer Modern Roman. Dette ble fÞrst endret i forbindelse med EU-standardiseringen samme Är.
Alan Turing? CERN 1991? Hmm...., noen prĂžver Ă„ vĂŠre morsom. Tror jeg. ?