Hei lillelørdag!

Her kommer en slags oppfølging til forrige ukes Formelfredag, som jo handlet om Pytagoras – som sier at \(katet^2 + katet^2 = hypotenus^2\). Jeg kommer tilbake til dette med Pytagoras lenger ned i dette innlegget, men først må jeg bare gi dere oppskriften på arealet av et kvadrat:

 

Oppskrift

 

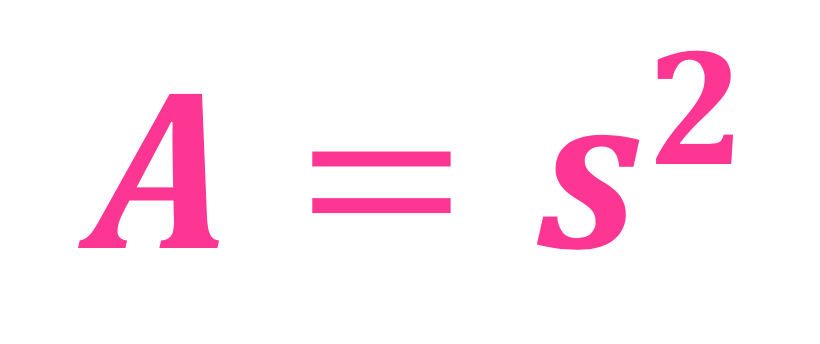
Hva det betyr

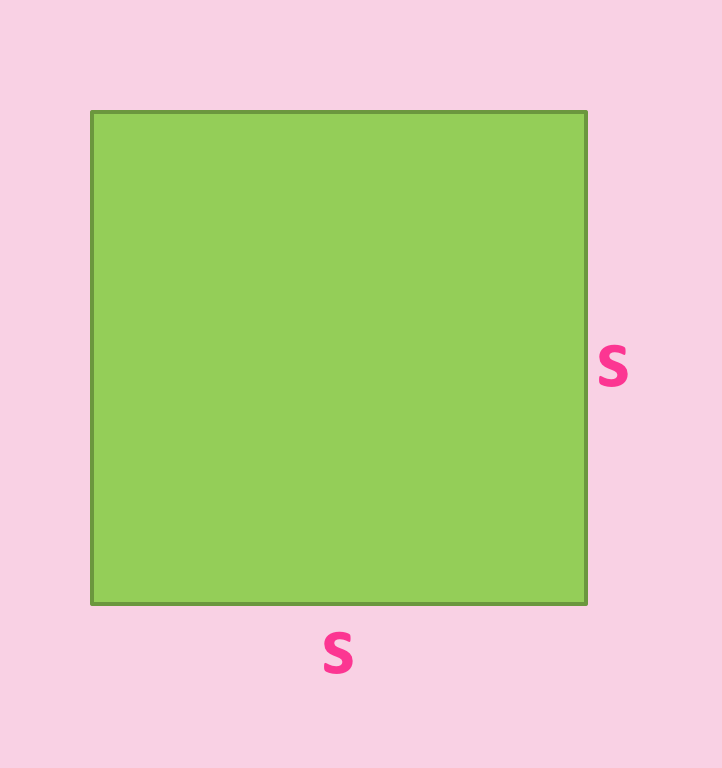
Et kvadrat er en firkant der alle sidene er like lange. Jeg kaller sidene for "s" i figuren under (hvis de ikke var like lange kunne jeg ikke kalt begge for "s" 😉 ). Arealet av en hvilken som helst firkant er lengde ganget med bredde, men i spesialtilfellet kvadrat så er jo lengden og bredden akkurat like lange, og dermed blir det s ganget med s som er det samme som \(s^2\).

A står for areal 🙂

Fremgangsmåte

Dette er jo en veldig enkel formel, og fremgangsmåten blir tilsvarende lett: Hvis s = 5 så blir arealet \(5 \cdot 5=25\).

Hva det betyr 2:

Grunnen til at jeg kaller dette en oppfølging av Pytagoras-innlegget er selvsagt fordi at når vi slår sammen Pytagoras og arealet for et kvadrat så står det faktisk at hvis vi lager kvadrater av alle sidene i en (rettvinklet) trekant, så er det sånn at arealet av de to korteste sidene i trekanten (katetene) blir nøyaktig like stort som arealet av kvadratet på hypotenusen (den lange siden). Pew, lang setning...

Og det ser sånn ut:

For å gjenta: Arealet av de to minste kvadratene i figuren over blir akkurat det samme som arealet av det størset kavdratet. Jeg syns det er helt sinnsykt fascinerende at det er sånn!

 

---

Nå skal jeg en tur ut med jentene - vi pleier å møtes på Mat og Mer, og det er litt ekstra stas igjen nå som ingen er gravide, og alle kan spise spekepølse og ta seg et glass vin (plis ikke skyt meg for å si at det er hyggelig at alle kan drikke – vær gjerne uenig, men sånn er nå min mening). Koselig blir det garantert, uansett! Vi snakkes ♥