Hei søndag og første pinsedag, og hei Formelfredag ♥
Her kommer tvillingsøsterinnlegget til absolutte og relative tall. Dette er også et slags irritasjonsinnlegg: Det syndes nemlig mye med prosent og prosentpoeng, og det irriterer meg, fordi det på ingen måte betyr det samme. Veldig ofte sier folk at noe har gått opp en eller annen prosent, når de mener at det har gått opp prosentpoeng: Feks hvis renten var 2%, og så gikk den opp til 4% prosent så sier mange at renten har gått opp to prosent, men det man egentlig mener er at renten har gått opp to prosentpoeng. Ja, her kommer pirke-Sunniva frem fra sinnaskallet sitt, og det HAR noe å si om man sier det ene eller det andre. Ikke noe poeng å være pirkete bare for å være pirkete, men å tulle med prosent og prosentpoeng betyr som regel helt VIDT forskjellige ting...
For å forklare eksempelet over litt nøyere: Hvis man betaler 2% rente, og denne går opp til å være 4% så har renten IKKE PÅ NOEN MÅTE gått opp 2%. Renten har gått opp 2 prosentpoeng (fra 2 til 4 er det 2: 2 + 2 = 4), eller sagt med andre ord, renten har gått opp 100% (en dobling, som er det som skjer her er det samme som at noe øker med 100%). Prosentpoeng er altså bare å se på tallet uten å ta med «prosent» - fra 2 til 4 er det jo 2, det har økt med 2 prosentpoeng. Fra 50% til 57% så er det 7 prosentpoeng. Prosentpoeng er det som er enklest å finne, mens hvor mange prosent noe har økt (eller minket) må man som regel regne ut.
Hvis man hadde 2% rente, og denne faktisk steg med 2% ville man ha endt opp med rente på 2.04% - altså mye mindre enn 4% 🙂 Når det er snakk om feks boliglån så er det ganske stor forskjell på om renten går opp til 2.04% eller om den går opp til 4% 😉
Forrige gang, da jeg skrev om absolutte og relative tall, snakket jeg jo om prosent, men ga egentlig ikke måten å faktisk regne på dette. Altså, prosent betyr jo egentlig "hundredel": Feks så er 1% av et eller annet det samme som 1 hundredel av dette et eller annet 🙂 Nå er det på høy tid å gi fullstendig oppskrift og fremgangsmåte på prosent:
Oppskrift
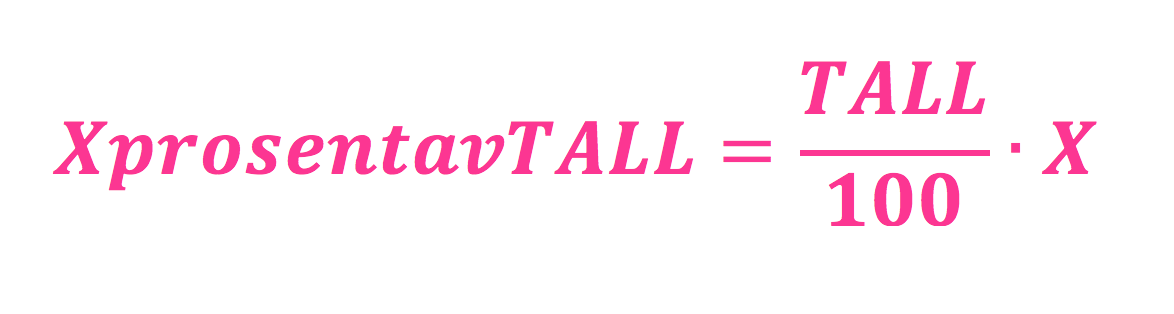
Hva det betyr
XprosentavTALL betyr at man skal finne en eller annen prosent (%) av et tall (TALL). X er for hvor mange prosent du vil finne - feks 2, 5, eller 100 (eller noe annet 😉 ). TALL er det man skal finne prosent av, X er altså hvor mange prosent, og 100 er 100.
Fremgangsmåte
Hvis vi skal finne 5% av 200, så er XprosentavTALL lik 5% av 200, TALL er 200, og X er 5:
5% av 200 = \(\frac{200}{100}\cdot 5\)
«5% av 200» betyr altså «5 hundredeler av 200", og det er akkurat det vi regner ut: Først, når 200 deles på 100 så finner vi én hundredel, så ganger vi den ene hundredelen med 5, og da har vi jo funnet 5 hundredeler av 200. Som altså er 10 🙂
Det er vel ofte snakk om at man skal kunne tåle 5 prosentpoengs økning på et boliglån - IKKE 5% økning. For oss, hvis jeg velger tall som er sånn ca riktige, så har vi i dag 2.5% rente på et lån på 5 millioner; det vil si 125 000,- (\(\frac{5000000}{100}\cdot 2.5\) = 125000)
5 prosent økning på renten betyr altså "pluss 5% av 2.5 (%)": \(2.5 + \frac{2.5}{100}\cdot 5 = 2.625\). Altså: 5% økning av 2.5% blir totalt 2.625% rente, som igjen betyr at vi måtte betalt 132 500,- i renter på lånet (\(\frac{5000000}{100}\cdot 2.625\)). Ikke all verden, med andre ord 😉
5 prosentpoengs økning, derimot, ville bety at vi fikk en rente som er 2.5% + 5% = 7.5% - altså 3 ganger så mye i renter som vi gjør i dag. 7.5% av 5000000 er \(\frac{5000000}{100}\cdot 7.5 = 375 000 \) På alle mulige måter noe å bry seg om! Det ER altså en forskjell på prosent og prosentpoeng, og det er IKKE bare Sunniva-pirk.
Ok, da tror jeg jeg er ferdig med å irritere meg for i dag, og jeg trooor jeg har fått frem et poeng (?), og skal gå tilbake til å bare være Sunniva som er overlykkelig over det fantastiske pinseværet, og at Anders hadde tid til å jobbe litt på café i dag før han dro på Blindern – aka. workdate ♥ Det er heldigvis bare 42 dager igjen til han leverer avhandlingen – noe jeg er overlykkelig over, og Anders er både lykkelig og ikke-lykkelig over på samme tid 😉
Jeg innser forøvrig at Anders og jeg ser ut som et gammelt ektepar - i alle fall på denne fine snapen som ble tatt av oss en dag rett før sommerværet plutselig slo til 😛


Takk for oppklarende innlegg, og generelt gode formelinnlegg:) Jeg husker vi jobbet med dette på ungdomskolen, og jeg syntes det var ganske forvirrende:P
Men, om jeg kan pirke litt tilbake, "Det er vel ofte snakk om at man skal kunne tåle 5 prosentpoengs økning på et boliglån - IKKE 5% økning.", skal det ikke stå at man skal kunne tåle 5% økning på et boliglån, og ikke 5 prosentpoeng, ettersom utregningen din etterpå viser at 5 prosentpoeng gjør at renta blir 7,5%? Eller er det jeg som surrer nå? Isåfall beklager jeg:)
Hei Camilla, og takk for kommentar, og takk for pirk 🙂
Jeg tror jeg har skrevet riktig: Poenget er nettopp at man skal tåle 5 prosentpoeng økning på renten, som altså er en stor økning - som jeg viser. Med dagens rente så betyr det at man ville måtte betale ca tre ganger så mye i renter som det man gjør i dag. Altså noe man virkelig merker...
Det skal ikke stå 5% økning på bolilånet - det er jo ikke lånet som øker, det er renta som kan øke, og da er det altså snakk om at man skal tåle at den øker med 5 prosentpoeng. Kun 5% økning på renten er lite, som jeg også viser 🙂
Håper dette var litt oppklarende!
Eller kanskje jeg misforsto deg?
🙂
Åjaaa, nå forsto jeg. Grunnen til at jeg påpekte det var fordi jeg mente at tre ganger økning hørtes forferdelig mye ut, som at det var for mye enn man skal kunne tåle. Men hvis det er meningen at økonomien skal kunne takle såpass stor økning så skjønner jeg hva du mente alikevel:)