Formelfredag: Tyngdekraft/Newtons gravitasjonskraft

Etter å ha sittet og snakket om kunstig tyngdekraft igjen for noen dager siden (link) slo det meg at det var rett og slett bare én eneste mulighet for denne ukens Formelfredag... Altså, jeg vet ikke hvorfor jeg ikke har tenkt på det før, men her kommer det altså: TYNGDEKRAFT. Tyngdekraften er jo viktig - den holder oss her nede på jorden og gjør at månen går i bane i bane rundt oss selv. Den får også planetene til å gå i bane rundt solen, og solsystemet vårt til å bevege seg gjennom galaksen vår ♥♥♥

 

- oppskrift -

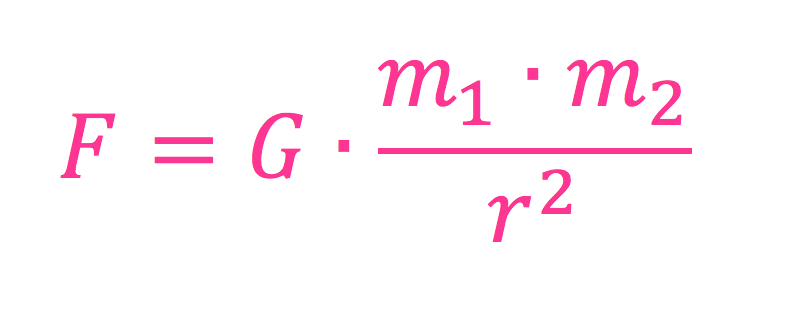
- hva det betyr - 

Det var Isaac Newton som fant ut av denne formelen på 1600-tallet, og publiserte den i 1687. Det denne formelen gjør er at den regner ut den kraften som virker mellom to objekter, for eksempel jorden og månen, eller deg selv og jorden,  som har hver sin masse, som vi kaller \(m_1\) og \(m_2\).
\(m_1\) og \(m_2\) står altså for massene til de to objektene (målt i kg). r er avstanden mellom dem (målt i meter - som alltid, hvis ikke blir det krøll 😉 ), og siden den står \(r^2\) (r i annen) så betyr det \(r\cdot r\), og G er den universelle gravitasjonskonstanten som man har funnet ut at er (ca) 6.67428×10⁻¹¹ m³⋅s^-2⋅kg⁻¹. F er altså den kraften man regner ut, og som tidligere så betyr også her F kraft (på engelsk heter det force) 🙂

 

- fremgangsmåte -

 

Det er to hovedting å huske på fra formelen: 1) kraften blir større hvis objektene har stor masse (jo mer de veier, desto større blir tyngdekraften/gravitasjonen), og 2) kraften blir mindre hvis avstanden mellom de to objektene blir stor. Det virker jo egentlig (kanskje?) intuitivt at tunge ting har mer gravitasjon enn lette ting (jorden vs månen). Og ting veeeldig langt unna hverandre påvirker ikke hverandre så mye - men de påvirker hverandre faktisk litt.

Såh, da er det bare å finne to ting du vil regne ut tyngdekraten i mellom, f. eks. Alexandra og Mars. Det eneste man trenger å vite da er hva Alexandra veier (\(m_1\)), hva Mars veier (\(m_2\)), og hvor langt det er mellom Alexandra og Mars (r):

\(m_1 = 20\) kg

\(m_2 = 6.39 × 10^{23}\) kg (som er det samme som 639000000000000000000000 kg) - her er det kanskje fristende og begynne å måle i tonn isdetefor kg, men det må man ikke finne på å gjøre - da blir alt bare feil 😉

\(r = 225 \ \text{milliarder meter} = 225×10^9 m\) (siden det varierer hvor langt det er mellom Mars og Jorden/Alexandra bruker jeg her gjennomsnittsavstanden).

Kraften (F) blir dermed

\(F = G\frac{20\cdot 6.39\cdot 10^{23}}{ (225\cdot 10^9)^2 } N = 6.67\cdot 10^{-11}\frac{20\cdot 6.39\cdot 10^{23}}{5.0625\cdot 10^{22} } N = 1.68\cdot 10^{-8} N\).

Kraften måles som vanlig i Newton (N). Dette er den kraften Mars drar med på Alexandra, når hun er 225 millioner km unna Mars, og det er denne kraften Alexandra drar på Mars med - det er ganske kult at det går akkurat like mye begge veier, syns jeg 🙂 Men hvor mye er nå dette? Det er omtrent samme kraften som tyngdekraften 1000 celler opplever fra jorden - altså veldig, veldig lite.

Til slutt har jeg lyst til å stille et spørsmål, og svar gjerne i kommentarfeltet her eller på Facebook eller på Snap (sunnivarose): Hvordan kan vi bruke denne ukens formel og få ut at akselerasjonen her på jordoverflaten er 9.81 m/s^2 slik jeg har påstått i flere innlegg nå? (Hint: husk på at Newtons andre lov også fins 😉 )

---

Her er forresten grunnen til at det ikke ble noen Formelfredag på fredag (ja, jeg har helt klart et planleggingsforbedringspotensiale - det er jo ikke som om at jeg ikke vet at fredag kommer hver uke...) - jeg var konfransier for årsfesten til hele Fakultetet, og det var en utrolig gøy kveld!

 

PS: I 1915 publiserte Einstein den generelle relativitetsteorien som er enda mer nøyaktig enn Newtons gravitasjonslov, men Newtons lov er allikevel mer enn god nok for å sende folk til verdensrommet, og beregne de fleste planetbaner (Merkur er et unntak).