Hei dere ♥ I går ble det dessverre ikke noe innlegg, for jeg trengte hele dagen på å forberede meg til dobbelforelesningen jeg holdt på Stipendiatkonferansen med Diabetesforeningen (i går ettermiddag/kveld), og da jeg kom hjem var mamma hos oss, og klokken var åtte og det var tid for Alexandra-legging, mat og The Handmaid's Tale (Og My...!), og så var det plutselig voksen-leggetid. Det var jo 26. april, som betyr Tsjernobyl-jubileum, og jeg får gjøre det godt igjen med å skrive om hvordan de aller fleste faktisk har fått lave stråledoser, som ikke er forbundet med sykdom (som f.eks kreft), en annen dag. Kanskje det kan være interessant med et innlegg om de arbeiderne som faktisk fikk STORE doser (som dessverre tok livet av dem), og hva som skjer i kroppen når sånt skjer, også?

Nok om gårsdagen, og over til fokus på dagen i dag; fredag og formeltid. Siden vi hadde annengradslikning forrige uke kan vi endelig fortsette med det fysikere (i alle fall jeg, som syns at sånn klassisk mekanikk er top of the pops) nemlig strekning og fart og tid. Storesøsteren til den veldig søte s = vt (som du kan lese mer om i DETTE INNLEGGET), som alle har lært på skolen, nemlig strekning, fart og tid, når du AKSELERERER (med formelen s = vt er det samme fart hele tiden - altså ingen akselerasjon ;)). jeg tror vi rett og slett bare bretter opp ermene og setter i gang:

Oppskrift

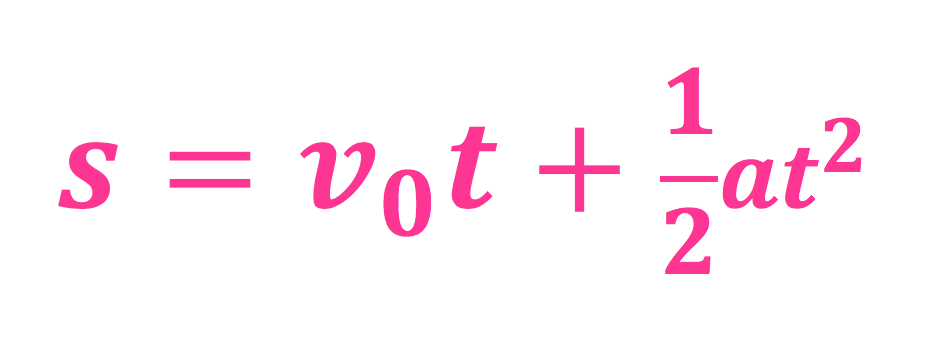
Hva det betyr

s betyr strekning,\(v_0\) leser man som "v null", og det betyr startfarten, t er tid (som alltid 😉 ), \(t^2\) er tid ganget med seg selv, og a er akselerasjon. Dette er oppskriften for hvor langt (strekning) noe beveger seg når det først har en eller annen fart i en viss tid, og så akselerer det en viss tid.

Fremgangsmåte

Hvis vi bare vil vite hvor langt noe beveger seg så er det ganske rett frem - startfarten er 0 m/s, akselerasjonen på jorden er 9.81 m/\(s^2\), og tiden er 10 sekunder (dette betyr at man tar et eller annet, en stein, feks, og slipper den fra et eller annet sted, og så finner man hvor langt den har falt etter 10 sekunder). Det blir seende sånn ut: \(s=(0\cdot10)+(1/2\cdot9.81\cdot10\cdot10)\), som blir \(s=0+490=490\). Hvis du slipper en stein, og den faller i 10 sekunder så beveger den seg altså nesten en halv kilometer (490 meter)! 🙂 (Jeg har forresten satt parenteser rundt de tingene som hører sammen, for det er mye ryddigere og enklere å vite sikkert hva som skal ganges med hva, og hva som skal plusses sammen når man rydder på den måte - litt på samme måte som jeg elsker å organisere ting som hører sammen i zip lock-poser :D)

Når du i stedet vil vite hvor lang tid det tar før steinen har beveget seg for eksempel 20 meter trenger vi plutselig ABC-formelen fra forrige Formelfredag. Hvis startfarten er 1 m/s, akselerasjonen er 9.81 m/\(s^2\), og strekningen er 20 meter, så kan vi finne ut hvor lang tid det tar (for hva nå enn å bevege seg 20 meter, altså): \(20=(1\cdot {t})+(1/2\cdot9.81\cdot{t^2})\). Nå har vi plutselig en annengradslikning, der den ukjente kalles for t istedetfor x, men det spiller selvsagt ingen rolle. For å løse denne gjør vi sånn:

Først setter vi den opp på riktig måte - så vi kan bruke ABC-formelen: \(1/2\cdot9.81\cdot{t^2}+1\cdot {t-20}=0\), og da blir a = 4.905 (1/2 ganget med 9.81), b = 1, og c = -20

Så er det bare å putte inn i formelen, og da blir det sånn: \(t=\frac{-1\pm\sqrt{1^2 - 4\cdot(4.905\cdot (-20))}}{2\cdot 4.905}\),  som blir \(t=\frac{-1\pm\sqrt{1 - (-392.4) }}{9.81}\)

og videre  \(t=\frac{-1\pm\sqrt{1 +392.4 }}{9.81} =\frac{-1\pm\sqrt{393.4 }}{9.81}\)

og til slutt så får man at t kan være to forskjellige ting (siden det står pluss/minus - \(\pm\)): den ene løsningen blir at \(t = \frac{-1+\sqrt{393.4 }}{9.81} = \frac{-1+19.83}{9.81} = \frac{18.83}{9.81} =1.9199\)

og den andre løsningen blir at \(t = \frac{-1-\sqrt{393.4 }}{9.81} = \frac{-1-19.83}{9.81} = \frac{-20.83}{9.81} =-2.1233\)

Begge løsningene, altså både at t = 1.9199 og at t = -2.1233 er matematisk riktige, men det er bare én som er fysisk riktig... Siden tiden kan ikke være et negativt tall (vi startet jo å slippe steinen ved t=0), så betyr det at det tar ca 1.92 sekunder for steinen eller ballen eller vesken eller hva nå enn å falle 20 meter 😀 Den andre løsningen vil vi også kunne få, men det kommer vi tilbake til senere 🙂

---

Nå er det virkelig bare å kose seg med strekning, fart, tid og akselerasjon - det anbefales ♥♥♥ #anbefalingmenikkespons #formlererbestingenprotest

Gooood helg alle fine!