Hei, fine lesere ♥ Her kommer ukens formel - endelig på en faktisk fredag 😀 Det er jo ingen ting å vente på, så vi skal kjøre rett på, men vil bare nevne at nederst i dette innlegget er det en ny, liten #tallpåting: hvor mye stiger Mjøsa hvis du putter alle mennesker i verden opp?
Ok, da er vi klare!
oppskrift
hva det betyr
På venstre side av er lik-tegnet står det \(\rho\), som er et gresk tegn som uttales "ro", og her står det for massetetthet (eller, ofte sier man bare tetthet, også). Grunnen til at jeg sier "her står det for" er at selv om \(\rho\) er symbolet for massetetthet (ikke bare akkurat her i dag, liksom), så er \(\rho\) også rett og slett en gresk bokstav, som i andre likninger kan stå for noe annet enn massetetthet.
På høyre siden står det m delt på V. m er for masse, som man måler i kg, og V er for volum, som måles i kubikkmeter. NBNB: IKKE i liter - hvis du har volumet av noe i liter må du (bør du) gjøre det om til kubikkmeter, for at ting ikke skal bli galt når du bruker det du regner ut videre i andre sammenhenger 🙂
fremgangsmåte
Hvis m = 500 kg, og V = 0.5 \(m^3\), så blir massetettheten:
\( \rho=\frac{500}{0.5} = 1000 kg/m^3\). ...og dét er massetettheten til vann - når det er 4 grader (Celsius). Ja, tettheten forandrer seg gjerne når temperaturen forandrer seg 🙂
Til sammenlikning så er massetettheten til luft 1.2 \(kg/m^3\) (nede ved havnivå - tettheten av gasser forandrer seg ettersom hvor i atmosfæren man er), og helium har en massetetthet på 0.179 \(kg/m^3\). Da kan vi se det jeg snakket om i innlegget om 17. mai og helium: Luft er lettere enn vann, så når du heller vann i et glass faller vannet ned, og luften går opp. Men ikke minst så er helium lettere enn luft - faktisk er luft nesten 7 ganger tyngre enn helium, så da faller luften ned, mens heliumen MÅ gå opp 😉
Så nå blir spørsmålet, hvis jeg vil sette litt #tallpåting - og det vil jeg jo alltid - hvor mye stiger Mjøsa hvis vi tar alle mennesker i verden og putter dem oppi? (Hvis du ser HER, så ser du at en ekstra meter med vann på Mjøsa tilsvarer vekten av hele verdens befolkning). Da bruker vi denne ukens formel, men det er V vi må finne. Jeg liker først å sette opp likningen "riktig", og så sette inn det vi vet. For å få V alene blir formelen seende slik ut: \(V=\frac{m}{\rho}\).
Mennesker har mer eller mindre samme massetetthet som vann - altså \(\rho = 1000 kg/m^3\) , og hele verdens befolkning veier ca 420 millioner tonn - altså \( m=420 000 000 000 kg\). Da er det bare å sette inn: \(V=\frac{420 000 000 000kg}{1 000 kg/m^3}\), og da blir svaret rett og slett at volumet av alle menneskene i verden er 420 000 000 \(m^3\), eller kubikkmeter.
Fra forrige gang vet vi at arealet av Mjøsa er 362 kvadratkilometer, som er det samme som 362 000 000 kvadratmeter. Det siste spørsmålet da er: Når vi har 420 000 000 kubikkmeter med mennesker, som skal fordeles ut over 362 000 000 kvadratmeter. Hvor høyt blir det da? Jo, da da bruker jeg det at volum er grunnflate ganget med høyde, og siden jeg vet hva grunnflaten er (362 000 000 kvadratmeter), og jeg vet hva volumet skal bli (420 000 000 kubikkmeter), så er det rett og slett bare å ta 420 000 000 delt på 362 000 000, og da blir svaret 1.16.
Dette betyr at hvis vi tar alle mennesker i hele verden (ja, det er mer en 7.5 milliarder av oss), og putter dem i Mjøsa, så stiger den med litt over 1 meter. Mind blown, på meg i alle fall 😉

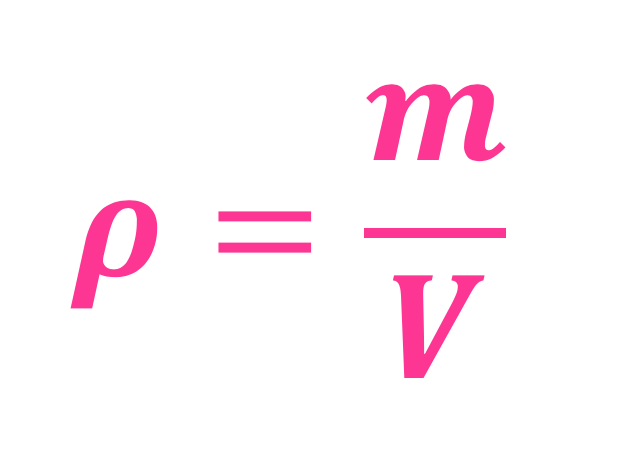
Mellom jobb og familie så pleier jeg ikke ha tid til å lese, og aller minst lete etter bra, blogger. Men kom over artikkelen i F&B om teppe på vognen og videre til bloggen. Gleder meg til å følge videre. Er selv geofysiker og begeistret over en intelligent blogg, og litt formel-fun-facts er midt i blinken altså!
Tusen takk, så hyggelig å høre!
Velkommen som leser 🙂