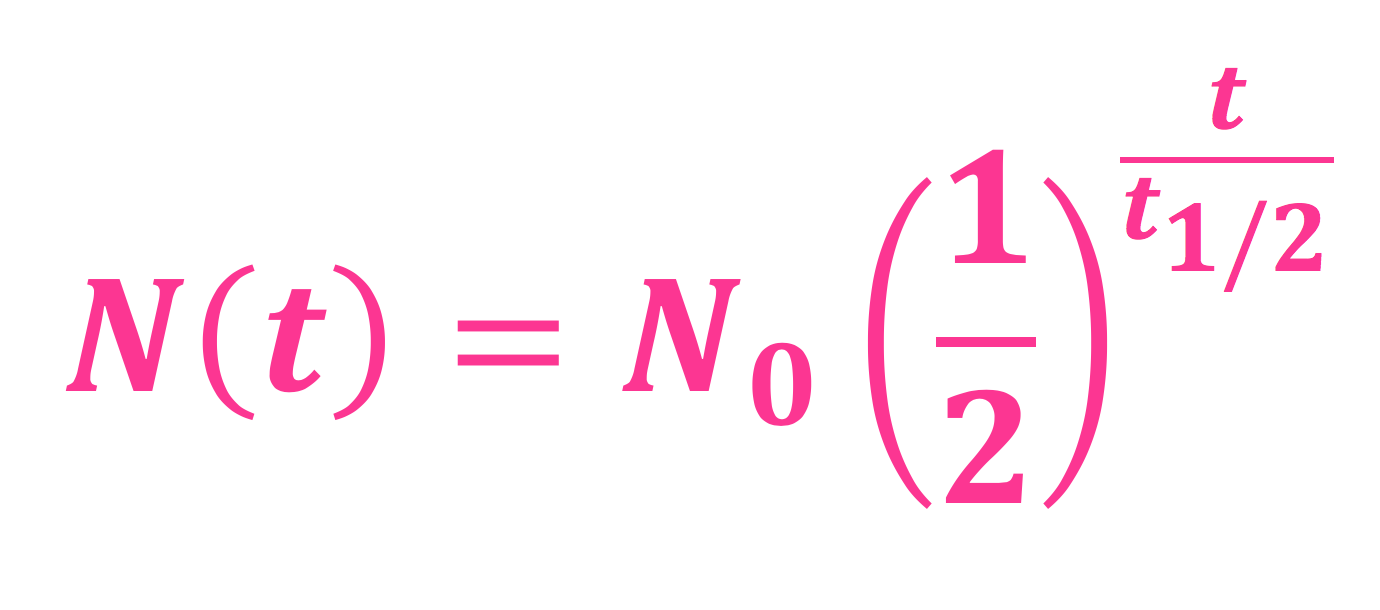Hei dere! Egentlig var planen at Formelfredag skulle gjennomføres i går (selvsagt - det var jo fredag 😛 ), men da jeg var nesten i havn ble jeg veldig usikker på noen beregninger jeg hadde gjort, og så følte jeg meg så utrolig dum, og så ble ALT bare dumt. Det endte med at jeg sto og hulket og gråt over hvor dum jeg er... Jeg orker ikke gå inn i akkurat hva det var akkurat nå, men heldigvis så kjennes det en god del bedre i dag (jeg kjenner meg ikke sååå dum lenger 😉 ), så det kan hende at den generelle formen min i går var medvirkende til mitt noe dramatiske utbrudd. Alexandra lurte veldig i dag på hvorfor mamma gråt og sa hun var dum i går etter at hun hadde lagt seg - jeg trodde selvsagt hun sov, men måtte jo bare si som sant er at følelser er en del av det å være menneske; glad, trist, sint, redd... Uansett, NÅ føler jeg meg klar for Formelfredag, og jeg har valgt ut en av mine absolutte favoritter - som jeg har jobbet litt ekstra mye med denne uken, nemlig Halveringstidsformelen ♥ Jeg har skrevet om den en gang tidligere, men den er så fin, og så mye brukt, at jeg tar den igjen 🙂
oppskrift
hva det betyr
Formelen forteller hvor mye det er igjen av et radioaktivt stoff hvis du starter med en viss mengde - feks 1 gram - etter en viss tid. N(t) betyr nettopp det - N er mengde (feks i gram), t er tid, og N(t) betyr mengde etter en tid.
\(N_0\) leses som "N null", og er mengden man har til å begynne med. 1/2 er en halv, t er fremdeles tid, og \(t_{1/2}\) er halveringstid.
Når man tar t og deler på \(t_{1/2}\) får man regnet ut hvor mange halveringstider som har gått: Feks, hvis halveringstiden er 5 sekunder, og det har gått 10 sekunder, så er vel alle enige i at det er det samme som 2 halveringstider...? Det er akkurat dét man får når du tar 10 delt på 5 - det blir 2; altså, det har gått 2 halveringstider 🙂
fremgangsmåte
Hvis du har 1 gram til å begynne med, av et radioaktivt stoff - feks radium-226 - og halveringstiden 1600 år, og så går det 4800 år - hvor mye har du igjen?
\(N_0\) = 1, \(t_{1/2}\) = 1600, og t = 4800, så da er det bare å sette igang å regne ut:
\(N(4800)=1\cdot(1/2)^{4800/1600}\)4800/1600 = 3, og dermed blir det videre:
\(N(4800)=1\cdot(1/2)^{3}\)\((1/2)^3\) betyr en halv ganget med en halv ganget med en halv (en halv ganget med seg selv tre ganger, altså), og det blir 1/8. Og det er det man har etter 4800 år; da har det gått tre halveringstider, og da har man 1/8 igjen av det man opprinnelig hadde. Siden vi startet med ett gram, betyr det at vi har 1/8 gram igjen av radium-226 etter 4800 år 🙂
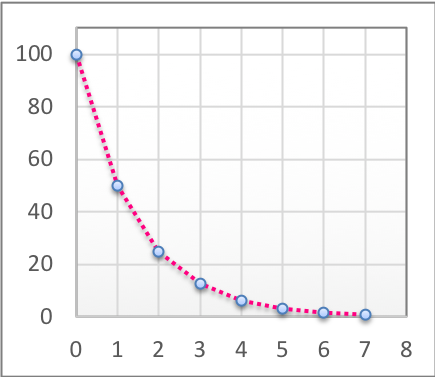
Den pene grafen under her viser hvordan dette med halveringstid og mengde ser ut: På x-aksen står det 1, 2, 3, osv, og det er da hvor mange halveringstider som har gått. På y-aksen står det 20, 40, osv opp til 100, og det er hvor mange prosent man har igjen. På starten, før det har gått noen tid har man selvsagt alt - 100%. Når det har gått én hel halveringstid så har man igjen halvparten, altså 50% (eller 1/2). Når det har gått enda en halveringstid så har man halvparten av dette igjen, altså halvparten av 50% som blir 25% (eller 1/4) 🙂
En vanlig misforståelse er at man tenker at etter én halveringstid så er halvparten borte, og etter én halveringstid til så er den andre halvparten borte... Men sånn er det altså ikke, for man får bare halvparten, så halvparten av det man har igjen, så halvparten av det man har igjen etter det, også videre - og da ser det altså sånn ut:
Vanligvis har jeg en streng policy på likninger når jeg holder foredrag - de skal ikke slenges opp uten at det er en VELDIG GOD GRUNN... Denne uken, da jeg snakket om forskningen til Ellen Gleditsch (Norges 2. kvinnelige professor, og en pionér på mange måter - ikke bare som kvinne), da hadde jeg faktisk med 2 formler; halveringstidsformelen var en av dem. Grunnen til det var at det kanskje aller viktigste arbeidet til Gleditsch var at hun fant halveringstiden til radium-226, og for å virkelig skjønne hva dette betyr, og hvorfor det er viktig, syns jeg det var riktig å gå i dybden på halveringstid. Som sagt, så gjort 🙂
Nyt lørdagskvelden ♥