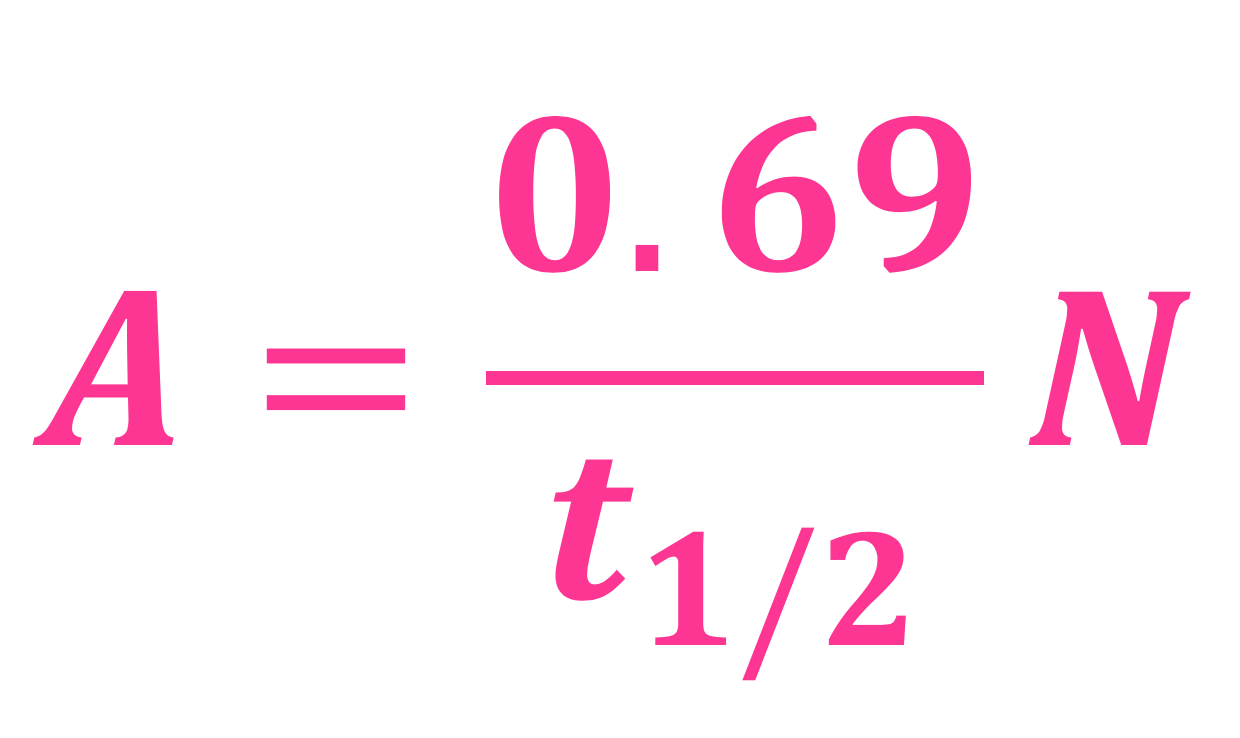Den andre formelen jeg hadde med i Ellen Gleditsch-foredraget forrige uke er nå klar for å skinne som ukens formel ♥ Det er selvsagt formelen for radioaktivitet!
Det som er et viktig poeng med radioaktive stoffer og halveringstid og sånn, er at et stoff som har lang halveringstid ikke er spesielt radioaktivt...! Dette er jo en ganske vanlig misforståelse, at man tror det at når noe har veldig lang halveringstid så er det KJEMPEFARLIG, men så er det altså ikke sånn. Jo kortere halveringstid, desto mer radioaktivitet:
oppskrift
hva det betyr
A står for aktivitet, eller radioaktivitet – og det forteller deg hvor mange atomer som hvert sekund sender ut stråling, i en eller mengde/klump. (Radio)aktivitet måles i bequerel, som rett og slett betyr "per sekund", eller "antall stråling utsendt per sekund".
Tallet 0.69 er egentlig ikke 0.69, men den naturlige logaritmen til 2, som er ca 0.69 😉
T1/2 er halveringstid (som måles i sekunder) – og det er den tiden det tar før halvparten av stoffet (klumpen/mengden) har sendt ut stråling. N er antall partikler (atomer) i den klumpen du har med radioaktivt stoff.
fremgangsmåte
Som sagt øverst i innlegget, så betyr "lang halveringstid" "lite radioaktivt", og "kort halveringstid" "mye radioaktiv". Hvis du feks sammenlikner radioaktiviteten i uran-238, karbon-14, og polonium-210 kan du se det ganske tydelig:
Hvis du starter med uran-238 først, så har denne en halveringstid 4.5 milliarder år.
1 år er 365 dager, ganget med 24 timer, ganget med 60 minutter, ganget med 60 sekunder, det vil si \(365 \cdot 24 \cdot60\cdot60\), så da blir halveringstiden til uran-238 142000000000000000 sekunder (\(1.42 \cdot 10^{17}\)) . 1 gram uran-238 har 2520000000000000000000 atomer (\(2.52 \cdot 10^{21}\)). Hvordan man regner ut hvor mange atomer det er i ett gram av et eller annet grunnstoff kan jeg gå igjennom en annen gang 🙂 .
Da blir radioaktiviteten i ett gram uran-238: \( \frac{0.69}{142000000000000000} \cdot 2520000000000000000000 =12245\) Bq (bequerel). Det betyr at ett gram uran-238 i snitt sender ut 12245 (alfa)partikler hvert sekund 🙂
Så kan du gjøre det samme med karbon og polonium:
Halveringstiden til karbon-14 er 5730 år, som er det samme som 180701280000 sekunder. I ett gram karbon-14 er det 42800000000000000000000 (\(4.28 \cdot 10^{22}\)) atomer. Da blir radioaktiviteten i ett gram karbon-14: \( \frac{0.69}{180701280000} \cdot42800000000000000000000 =163429943606\) Bq. Ett gram karbon-14 sender ut ca 163 milliarder (beta)partikler hvert sekund.
Halveringstiden til polonium-210 er 138 dager, som er det samme som 11923200 sekunder. I ett gram polonium-210 er det 2850000000000000000000 (\(2.85 \cdot 10^{21}\)) atomer. Da blir radioaktiviteten i ett gram polonium-210: \( \frac{0.69}{11923200} \cdot2850000000000000000000 =165000000000000\) Bq. Ett gram polonium-210 sender ut ca 165000 milliarder (alfa)partikler hvert sekund.
Jeg tror man kan se ganske klart her nå at polonium-210, med sin korte halveringstid, på bare noen dager, uten tvil er det mest radioaktive stoffet. Polonium-210 var forresten det stoffet som ble brukt til å forgifte og drepe den tidligere russiske KGB-agenten, Alexandr Litvinenko, i London i 2006.