
Wow, denne uken ha gått fort…! På tirsdag ledet jeg Forsker Grand Prix, og dermed forsvant mandagen til forberedelser til dette, tirsdagen forsvant naturlig nok på Latter (der Forsker Grand Prix ble avhold), og onsdag til å gjøre alt “forefallende” fra tirsdagen, og hva som skjedde med gårsdagen er jeg ikke 100% sikker på. Så jeg er kanskje litt treg når jeg nå forteller at vi kjørte til Hamar på søndag, men dette er liksom første "muligheten". Grunnen til at jeg nevner det er fordi da vi kom til Mjøsa begynte vi å snakke om hvor stor den innsjøen faktisk er, og ganske fort dukket spørsmålet opp: Er Mjøsa så stor at du ikke kan strekke et tau over uten at det går ned i vannet, på grunn av at jordoverflaten er krummet (aka jorden er rund)?
(Hvis du bare vil ha svaret uten utledning og likninger kan du scrolle til slutten av innlegget 😉 )

Og da mener jeg selvsagt at vi later som at vi kan holde et tau så stramt at det ikke “siger nedover”, så tauet er absolutt helt stramt og rett - går det da allikevel ned i vannet?

Det går ikke an å trekke et tau fra Lillehammer til Minnesund fordi Mjøsa svinger seg, så da må det bli ca som på kartet:
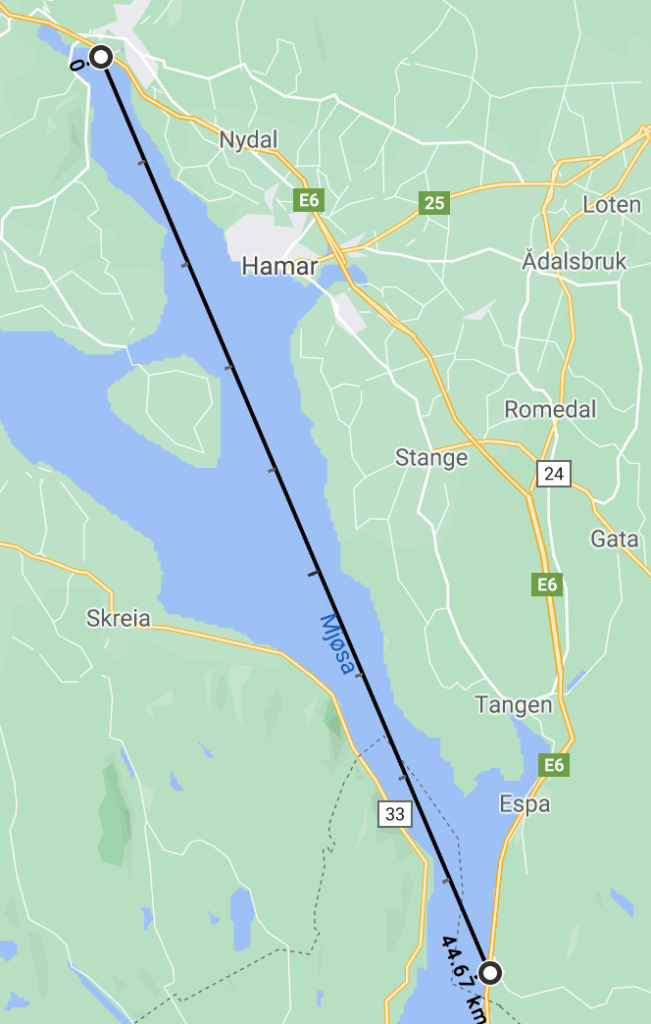
Altså omtrent 45 km. Omkretsen på hele jordkloden er 40 075 km, og radius på jorden er 6 371 km.

Med disse tallene kan man finne ukjente vinkelen, som jeg har gitt det klingende navnet V - forholdet mellom lengden på Mjøsa og hele jordens omkrets, og vinkelen V og hele sirkelen (360 grader) er nemlig det samme:
45 km / 40075 km = V/360
V = 360 * (45 km /40075 km)
V = 0.40424204616 grader (Ja, her er det faktisk ordentlig viktig å ha med MANGE desimaler for å få riktig svar til slutt 🙂 )
På tegningen under har jeg tatt med noen flere detaljer: Den stiplete linjen er rett linje fra den ene siden av Mjøsa til den andre - siden vi vet at jorden ikke er flat så vil selvsagt en sånn rett linje gå noe under vann, spørsmålet er om det er så mye at vi ville ha merket det på dette tauet jeg vil strekke over. Det er på midten det vil gå mest ned i vannet, og spørsmålet er hvor langt under vann dette blir - det er det som er den ukjente høyden, som selvsagt får navnet X.
På denne tegningen er alt selvsagt veldig overdrevet, for at det skal være mulig å se de forskjellige detaljene 😉
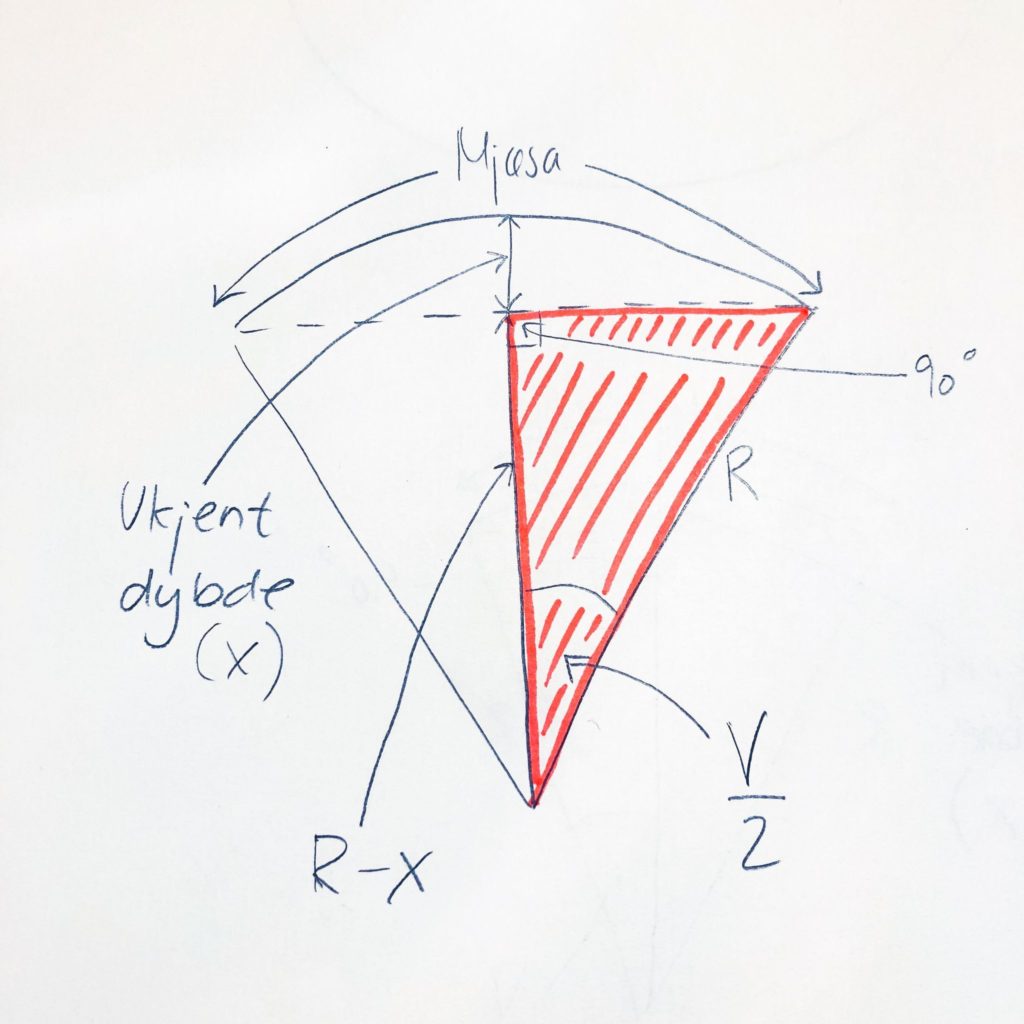
Måten vi kan finne X på er ved å se at vi har en trekant (rød), der vi både vet hva vinkelen er (V/2, altså halvparten av den vinkelen vi nettopp regnet ut: 0.20212102308), og hypotenusen (R, radius på jorden). Den siden på trekanten vi trenger har lengde R-X, som vi kan finne ved å bruke cosinusfunksjonen:
R - X = R * cos(V/2)
R - X = 6375 km * 0.99999377775
R - X = 6374.9603 km
X = 6375 km - 6374.9603 km = 0.0397 km
Altså betyr det at hvis vi strekker et tau over Mjøsa sånn som på kartet så er det ikke bare sånn at krummingen på jorden gjør at tauet blir litt vått. Tauet ville ligget omtrent 40 meter under vannflaten fordi jorden er rund. Sånt syns jeg (og Anders) er ganske kult!
Grunnen til at vi kjørte til Hamar var blant annet at jeg skulle være gjest i podcasten Nordpodden, og den episoden kan du høre på (og evt) se her 🙂


Hvis du sitter i en liten båt midt ute på et stille og speilblankt hav, øynene dine er 1 meter over vannflata, hvor langt unna vil horisonten (synsranda) være da?
Kvadratroten av høyden x 2 = nautiske mil, dvs med 1 meter øyehøyde = 2.n.m. = 3,7 km.
For å se over hele Mjøsa må du 145 m opp i høyden.
Heia Jeppe. Dette kan du!
Hei Petter, dette er et fint oppfølginsspørsmål til dette innlegget! Jeg tar dette i et eget innlegg (antageligvis) i løpet av uken som kommer. Stay tuned 🙂
Hei, har 3 rosa døtre som jeg har tenkt å kjøpe boka til. Kommer du til å signere den hos noen bokhandlere?
Hei John Egil, så utrolig hyggelig at vil kjøpe boken min!
Det er ikke planlagt noen signering ennå, så vidt jeg vet om, men send meg en mail så fikser vi alltids en signert bok (eller 3) 🙂
Herlig nerdete, sånn liker vi
😀
Flott! Da gjenstår det bare å strekke tauet og la flatjordfolka verifisere målingen, så får vi se hvilken fantasifull forklaring de da kommer med.
Haha, ja, jeg antar de har en "forklaring" samme hva...
Hehe...😅🤠
Et fantastisk praktisk eksempel som definitivt burde ha vært i ei matematikkbok på ungdomsskolen/videregående. Satte meg ned og regnet igjennom eksempelet for å kunne bruke eksempelet i en eller annen sammenheng senere... Har to forbedringspotensialer...
1. At du mikser R=6371km og R=6375km (bagatell for svaret)
2. At du ikke kompenserer for de 121moh Mjøsa ligger (også en bagatell for svaret).
Også hadde det jo vært supert om en eller annen wireprodusent kunne stille med 45km wire slik at det kunne prøves i praksis (da selvfølgelig kompensert for sig
Hei, og takk for korreksjoner! Ja, jeg var visst litt trøtt da jeg satt og skulle få dette på plass - sånt skjer (men bra for deg som leser, så må du følge litt ekstra godt med 😉 😛 ).
Jeg er helt enig at vi definitivt burde gjennomføre dette som eksperiment 😀
La oss prøve med en laserstråle I stedet...😉
Tenk at du trekker et tau fra et punkt på ekvator, rett over (geografisk) Nordpolen og til ekvator på andre siden. Hvis du så strekker ut tauet (litt sånn som i Mjøsa eksempelet), hvor høyt/dypt er det da fra midten av tauet til Nordpolen? Svar: 6371 km!
....og dette løste jeg helt uten å bruke ligninger, vinkler og cos. .....imponerende, eller 🤓
Hehe 😛
Du har et veldig forenklet regnestykke!
jorda er tilnærmet en ellipsoide, store halvakse 6378137 m, lille halvakse 6356752,314 m
Dette er definert i EUREF89, det offisielle geodetiske datumet i Norge.
Likevel burde du heller brukt geoiden og gjort tyngdemålinger fra Lillehammer til Minnesund.
Erik S:
Vis oss hvordan du ville regnet ut dette for en ellipsoide. Tviler på at det har noen særlig betydning i praksis!
jeg regna mye på det for nesten 30år siden i geodesi-undervisning, men har dessverre glemt mange av formlene nå...
Håper sunnivarose har flere formler tilgjengelig 🙂
Takk for at du deler en slik informativ artikkel. Foliering kan brukes til å sette logoer eller annet budskap på ditt kjøretøy for å oppnå mer synlighet på veien. Folien vil skreddersys til ditt kjøretøy for å oppnå best effekt og øke profileringen av ditt selskap.
https://carmagic.no/tjenester/foliering/
Hei: Jeg har visualisert i autocad denne linjen gjennom Mjøsa fra Lillehammer til Minnesund og svaret jeg får er 83,4 meter ikke 40 meter som største differansepunkt mellom Mjøsoverflata og den horisontale linjen.