Etter Mjøsa-innlegget her om dagen, fikk jeg et spørsmål i kommentarfeltet:
Hvis du sitter i en liten båt midt ute på et stille og speilblankt hav, øynene dine er 1 meter over vannflata, hvor langt unna vil horisonten (synsranda) være da?
Det er jo et veldig fint spørsmål, og det er egentlig ganske enkelt å svare på, men tegninger er alltid kjekt å ha nesten uansett:
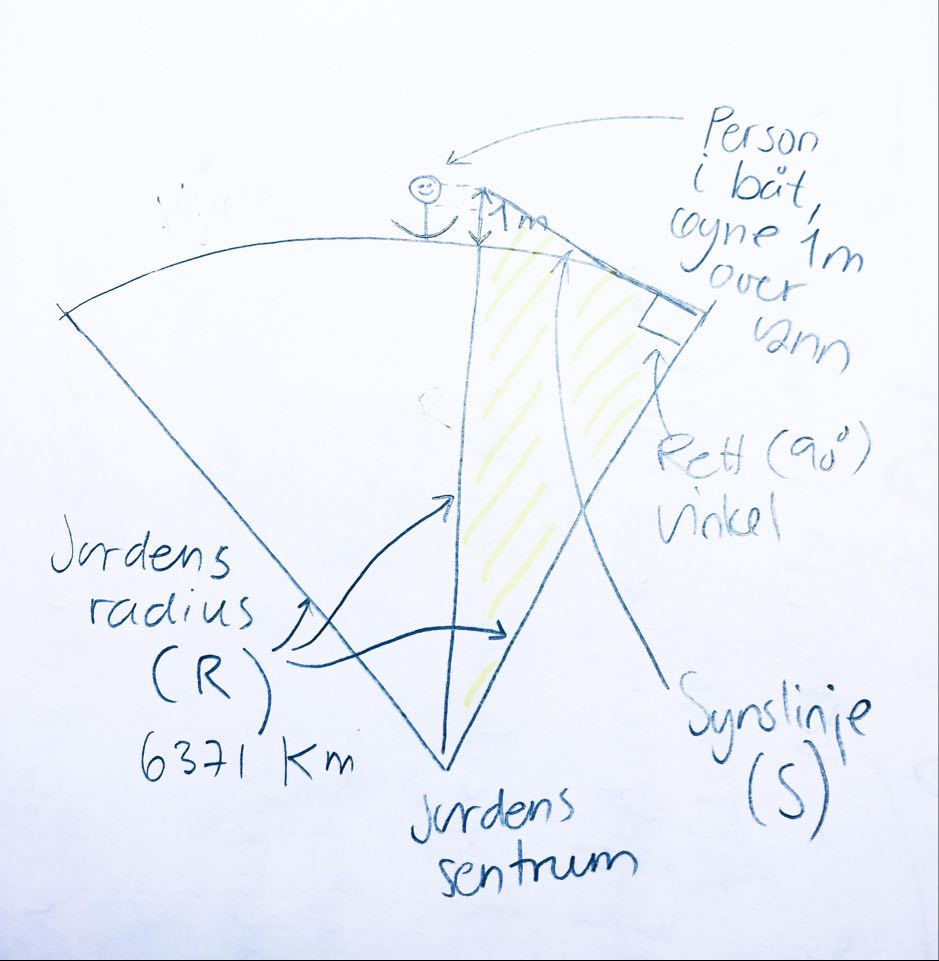
Jordens radius er fremdeles 6371 km, eller 6 371 000 m, mens jordens radius pluss personen er 6 371 001 m. Pesonen kan se i en rett linje bortover og nedover mot jordoverflaten, helt til synslinjen tangerer jordoverflaten. Det er denne synslinjen, som jeg har døpt S, som er ukjent. Når S tangerer jordoverflaten lager den en 90 graders vinkel med jordens radius, og dermed kan vi bruke gode, gamle Pythagoras til å finne ut av hva S blir.
Pythagoras sier at katet opphøyet i annen pluss katet opphøyet i annen er lik hypotenus opphøyet i annen.
I dette stykket er det R som er den ene kateten, hypotenusen er R+1 m, og S er den andre og ukjente kateten:
6371000*6371000 + S*S = 6371001*6371001
S*S = 6371001*6371001 - 6371000*6371000
S*S = 12742001
S = kvadratroten av 12742001 = 3569.6 m
Så svaret på hvor langt du kan se, eller hvor langt unna horisonten er, er ca 3.5 km.
Med andre ord: Du kan ikke se over Mjøsa på kartet der vi prøvde oss på å strekke tau. Eller, altså, du kan jo se noe på andre siden (trær og ting som er på land), men du kan ikke se vannflaten hele veien 🙂


Og så er det morsomt ar selvom unøyaktigheten på radien er feks. 500m så gir det bare et utslag på 0.1 m for synsavstanden
Ja, det er ganske kult 🙂
Bra fremstilt, grunnet kruming til jorden Sunniva
Ja, det kan generaliseres til
S = √(2hR)
S = √(12,7 × h) [km], h i meter