Hopp til innhold

Kategori: formelfredag

formelfredag

2

Publisert 2 kommentarer til God kveld, og oppfølging om vaskemaskiner og kunstig tyngdekraft

God kveld, bloggen ♥ Dagene går i ett, og to do-listene mine blir aldri skikkelig streket ut, men jeg må jo bare innom her så ofte jeg får til allikevel - altså, jeg "må" ingenting, men jeg VIL! I skrivende stund sitter jeg i den nye, fine, okergule lenestolen vi har skaffet til stuen og blogger altså. Stolen er fra IKEA, og jeg syns den ER SÅ FIN i tillegg til at den er skikkelig god å sitte i. Men ikke bare er den god å sitte i; den er også på vei til å bli min "blogge/generelt skrive-stol" - og jeg har allerede sittet her en veldig drøy time før jeg begynte å skrive dette innlegget, der jeg har jobbet på en sak om studenter og læring, og jeg lærer så mye om det å lære, og det er veldig spennende 🙂

Men nok om det akkurat nå (nå har jeg vært i min nye jobb siden juli, og endelig begynner jeg å få den såpass "under" huden at det er noe jeg føler jeg kan dele og skrive om på en skikkelig måte her, og da vil jeg heller ta det i egne innlegg, enn her nå) - over til et spørsmål jeg stilte på en formelfredag for en stund tilbake. I slutten av innlegget om Kunstig tyngdekraft spurte jeg:

En vaskemaskin, hvor fort må den snurre for å få nøyaktig 9.81 \(\frac{m}{s^2}\) akselerasjon?

...og nå er det på tide å avsløre svaret.

Vi starter med å vite at sentripetalakselerasjonen har denne formelen er \(a = \frac{v^2}{r}\), som blir det samme som at \({v^2} = a\cdot r\).

a har vi bestemt at skal være 9.81\(\frac{m}{s^2}\) (alstå akkurat den akselerasjonen vi har mot bakken hele tiden her på jorden), og radiusen til vaskemaskintrommelen kan man enkelt måle (hvis du har tilgang til en vaskemaskin, og du har noe å måle med, feks en linjal eller tommetokk, da) - den er typisk 25 cm, eller i meter (som er det vi må bruke!) er den 0.25 m. Farten blir da rett og slett bare kvadratroten av 9.81\(\cdot \)0.25, og det er 1.56 m/s.

 

Dét er altså så raskt vaskemaskinen snurrer for at den skal lage "kunstig tyngdekraft", men det tallet sier kanskje ikke så mye...?

Heldigvis var det en leser som gikk litt lenger, og regnet ut hvor mange omdreininger per minutt denne farten (1.56 m/s) tilsvarer; nemlig ca 1 omdreining i sekundet. Konklusjonen fra dette er at det som er inne i trommelen opplever en kraft som er mye større enn 1G når den sentrifugerer, for det er ikke akkurat mye 1 omdreining per sekund når vaskemaskinen setter i gang sentrifugen! Et typisk oppfølgingsspørsmål er selvsagt hva slags akselerasajon opplever klærne i trommelen når den maskinen sentrifugerer maks (oppgi gjerne svaret i antall G)?

Nå er det kvelden her i nye Roseslottet; Anders har hatt en skikkelig lang dag på kontoret i dag (#phd), og nå tror jeg han snart er hjemme, så da er det kvelden her. Da er det bare å avslutte dagen med et Hurra for lesere som tar frem tommestokken og legger seg ned og måler radiusen på trommelen i vaskemaskinen - og regner seg frem til riktig svar 😀

 

3

Publisert 3 kommentarer til Formelfredag: Temperatur

Hei, og god fredag! Dere, denne ukens formel er superenkel: Jeg er egentlig vanligvis motstander av å komme med påstander om at noe er enkelt, men med akkurat denne er det sant. Superenkel, men også superviktig - det handler om temperatur.

Når man skal regne ut forskjellige ting der man skal putte inn temperatur (feks i termofysikk) så må man bruke denne formelen først, ellers blir alt bare feil... Er dere klare? Her kommer oppskriften:

- oppskrift -

 

- hva det betyr - 

T er temperatur, som altså ikke lenger er grader celsius, sånn som vi er vant med, men Kelvin (mer: IKKE grader Kelvin, bare Kelvin 🙂 ). C er den temperaturen du har målt, sånn vanlig i grader celsius, og 273.15 er tallet 273.15.

 

- fremgangsmåte -

Formelen forteller hvordan du går fra temperatur målt i grader celsius til Kelvin, og man tar rett og slett den temperaturen du har målt og legger til 273.15 - enklere enn det kan det vel ikke bli?

For eksempel: Hvis det er null grader (celsius) er dette det samme som 0+273.15=273.15 Kelvin.  Eller hvis temperaturen er -273.15 grader (celsius) blir det -273.15+273.15=0 Kelvin.

0 Kelvin er så langt ned man kommer, og det er det som kalles det absolutte nullpunkt. Negativ temperatur fins altså egentlig ikke, selv om vi snakker om minusgrader til vanlig. Når man kommer ned til 0 Kelvin slutter atomene å bevege seg; alt står bare stille (eller, altså, elektronene kan ikke stå stille, på grunn av Pauli-prinsippet, som man lærer om i kvantemekanikk - så heeeelt stille står ikke ting) 🙂

 

2

Publisert 2 kommentarer til Formelfredag: kunstig tyngdekraft

Ukens formel er egentlig ikke en ny formel, men endelig kan vi sette sammen ting fra tidligere innlegg, og løse praktiske problemer 🙂 Praktiske problemer av den typen du får når du skal være veldig lenge på et romskip, altså i vektløs tilstand. Med andre ord; ikke ting som er problemer for de fleste av oss...;)

I dette innlegget står det om Newtons andre lov, som kort fortalt sier at \(F = m\cdot a\), og i innlegget fra forrige ukes formel står det om sentripetalakselerasjon - altså den akselerasjonen man har når man kjører rundt og rundt i en sirkel: \(a = \frac{v^2}{r}\).

Sentripetalakselerasjon er nettopp det som gjør at vannet presses ut av klærne under sentrifugeringen i en vaskemaskinen. Trommelen snurrer rundt og de våte klærne går i sirkelbane inni maskinen. Det er små hull som gjør at vannet får lov til å renne ut mens klærne forblir på innsiden. Vått tøy minus vann er lik mindre vått tøy 🙂

I innlegget om Newtons andre lov skrev jeg om tyngdekraft. Hvis vi setter sammen idéen om sentrifugen med det vi vet om tyngdekraften på jorden har vi alt vi trenger for å finne ut hva slags romskip vi må ha for å lage "kunstig tyngdekraft" for astronauter i vektløs tilstand enten i bane rundt jorden eller kanskje på vei til Mars. Løsningen er nemlig at romskipet må ha en snurrende del sånn som dette:

Romskipet kan være formet som mye rart, men det viktige å få med seg her er den store donut'en (den er jo en slags sirkel med radius r). Hvis romskipet er vektløst vil en person som står inni kjenne at han/hun blir dyttet utover når det snurrer (tenk på tekoppen-karusellen 😉 ).

Vi kan nå kombinere de to formlene til å finne sammenhengen mellom radius på romskipet og farten det må snurre med for at en person inni opplever å bli dyttet mot gulvet akkurat like hardt som jorden drar deg ned mot gulvet. Vi starter med selve formelen

- oppskrift -

 

 

- hvorfor det blir sånn/forklaring -

Forklaringen kommer her (du kan gjerne hoppe over, hvis du ikke vil vite hvordan det er sånn, og gå rett ned til hva det betyr):

Newtons annen lov sier altså at \(F=m\cdot a\), og her på jorden er a (det som kalles tyngdeakselerasjonen) 9.81\(\frac{m}{s^2}\), så derfor blir tyngdekraften \(F=m\cdot 9.81\). Når du kjører i en sirkel så er \(a=\frac{v^2}{r}\), og siden du har en akselerasjon (som ikke er null), så blir den kraften du blir presset utover med \(F=m\cdot\frac{v^2}{r}\) (her starter man også med Newtons annen, og setter man inn \(\frac{v^2}{r}\) der det står a 🙂 )

Da har vi to forskjellige likninger som forteller om kraft: 1) \(F=m\cdot 9.81\), og 2) \(F=m\cdot \frac{v^2}{r}\). Poenget er at når vi er i det snurrende romskipet så vil vi at den kraften vi blir presset utover med skal være lik den tyngdekraften vi kjenner her på jorden, og derfor sier vi at \(F=m\cdot 9.81\) på en måte er fasiten - det er det vi må få på vestre siden av likhetstegnet i likning 2). Dermed blir det seende sånn ut: \(m\cdot 9.81=m\cdot \frac{v^2}{r}\). m er den samme på begge sider av likhetstegnet, så den kan vi bare ta bort (og det er jo litt heldig, for ellers ville det vært sånn at alle astronauter måtte hatt akkurat samme masse for at dette skulle funke, men heldigvis så er denne kraften uavhengig av massen din, eller det vi ofte kaller for vekt, da 😉 ). Så da ser det slik ut: \(9.81=\frac{v^2}{r}\), og fra denne får vi likningen over ♥

 

- hva det betyr -

 

Et romskip som i bildet øverst har en eller annen radius, og da kan vi bruke formelen for å finne ut akkurat hvor fort det må snurre for å få lik tyngdekraft som på jorden!

v er hastighet ("fart"), r er radiusen i den sirkelen du beveger deg i (radiusen til romskipet), og 9.81 er 9.81\(\frac{m}{s^2}\), eller det som kalles tyngdeakselerasjon som er det som gjelder her på jorden (ja, vi har faktisk hele tiden en akselerasjon ned mot bakken). Som alltid så må man måle hastigheten i m/s, og radius (eller en hvilken som helst avstand) i meter - ellers blir det bare krøll 😉

- fremgangsmåte -

Hvis vi har et romskip som har radius 100 meter (det er jo et ganske stort romskip, men fint tall å regne med). Da kan vi bruke formelen med én gang for å finne farten:\(v = \sqrt{r\cdot 9.81} = \sqrt{100 \cdot 9.81} = \sqrt{981} = \sqrt{981} = 31 \frac{m}{s}.\)

Det er jo egentlig ganske fort (111 km/t), men så var det jo et ganske stort romskip også. Å ha et stort romskip er viktig fordi et menneske er omtrent 2 meter, og vi vil jo ikke at føttene og hodet skal ha veldig forskjellig akselerasjon, så vi vil at menneskehøyden er liten sammenliknet med radien på sirkelen. Det kan jo hende et romskip som har halvparten så stor radius er greit nok, og da vil vi få farten

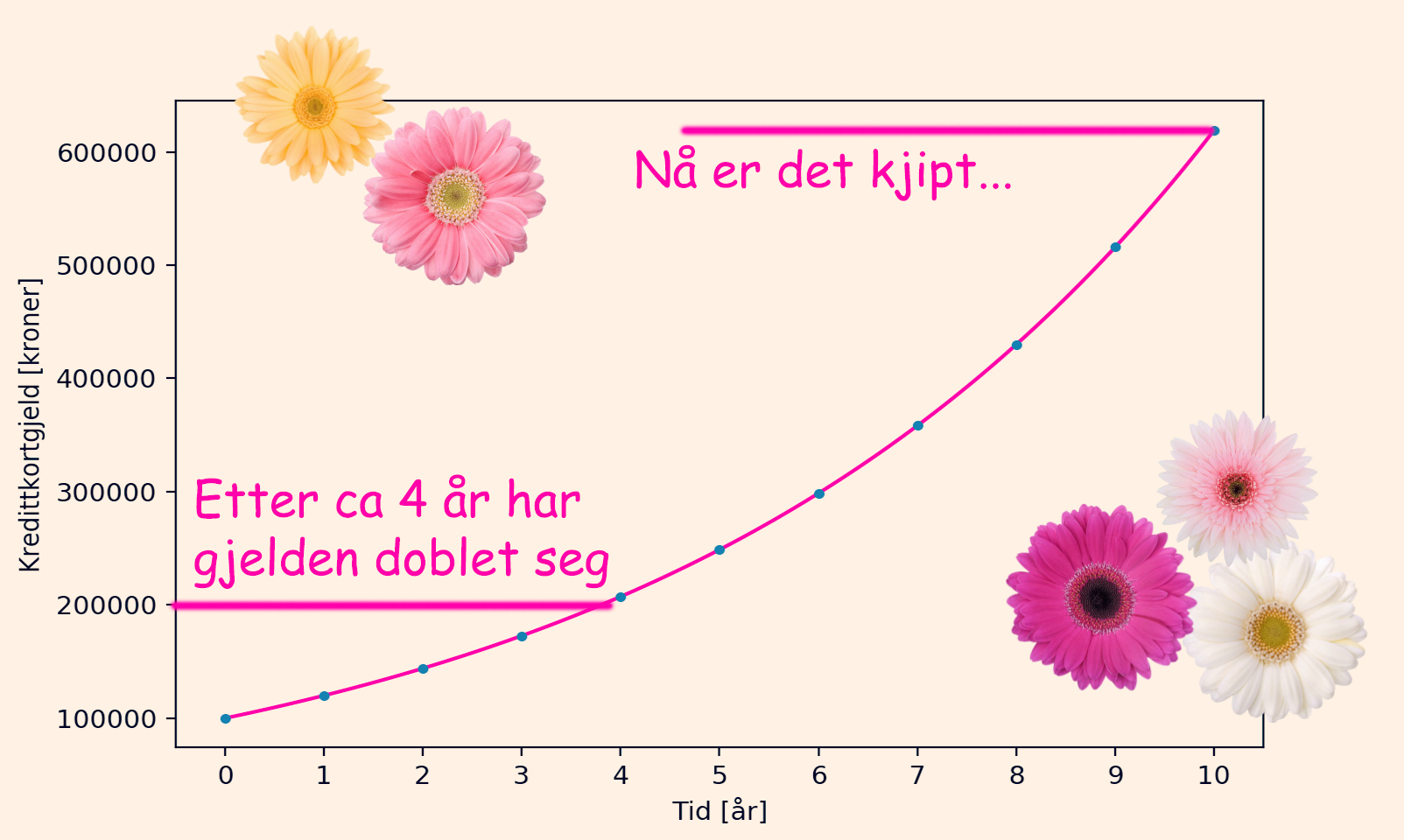
\(v = \sqrt{r\cdot 9.81} = \sqrt{50 \cdot 9.81} = \sqrt{490.5} = \sqrt{490.5} = 22.15\frac{m}{s}\), en god del lavere fart, men mer enn halvparten! Denne farten ser vi at stemmer fra grafen under. Hver rosa prikk i grafen viser hva farten må være ved forskjellige radiuser.

 

Men hvor fort må den snurre da? Da tenker jeg på antall omdreininger (bedre kjent som RPM, revolutions per minute), slik vaskemaskiner og bilmotorer ofte oppgir. Hvis du står i romskipet vil du jo i løpet av en hel runde bevege deg akkurat like mye som omkretsen på sirkelen. Omkretsen har formelen \(O = 2\pi r\), så i det første eksempelet er omkretsen

\(O = 2\pi r = 2\pi 100 = 2\cdot 3.14\cdot 100 = 628 m\). Når vi har farten 31 meter per sekund vil det jo ta \(\frac{628}{31} = 20\) sekunder å bevege seg en hel runde. På et helt minutt får vi 3 runder, altså 3 omdreininger i minuttet. For det litt mindre romskipet blir omkretsen \(O = 2\pi r = 2\pi 50 = 2\cdot 3.14\cdot 50 = 314 m\). Antall sekunder per omdreining blir da \(\frac{314}{22.15} = 14.18\), så omdreininger i minuttet blir \(60/14.18 = 4.23\), mer enn for det store romskipet.

Sånn helt til slutt, fordi det er en fin avslutning på formelfredag, og uken sånn generelt: En vaskemaskin, hvor fort må den snurre for å få nøyaktig 9.81 \(\frac{m}{s^2}\) akselerasjon? Skriv svaret i kommentarfeltet her eller på Facebook, eller send meg en snap, eller hva som helst ♥

 

Publisert Legg igjen en kommentar til Ukens formel: (sentripetal)akselerasjon

Denne uken er det ikke akkurat en formel, men mer kanskje en slags forklaring av noe som kanskje virker litt rart, nemlig akselerasjon. Akselerasjon er en del av blant annet Newtons andre lov. Den har enheten \(m/s^2\) som vi leser som meter per sekund i annen  - som betyr meter per sekund per sekund, egentlig. Dette kan kanskje være litt forvirrende, men det er absolutt en god grunn til at det nettopp er per sekund i annen (altså per sekund per sekund), og det skal jeg prøve å forklare nå! For å forstå hva denne enheten er kan vi begynne å tenke på hva fart egentlig er. En naturlig situasjon der fart er viktig er for eksempel på en løpebane.

Hvis du står akkurat der du startet står du 0 meter fra der du startet (d'oh 😛 ). Hvis du nå begynner å løpe med null fart flytter du ikke på deg. Du står på akkurat samme sted hele tiden. Hvis du har fart vil du forandre hvor du er. Så fart er endring av posisjon (forandring av der du er).

Enheten til fart er m/s (meter per sekund), noe som gir mening fordi det forteller deg hvor mange meter du flytter deg hvert sekund. Hvis du stod der du startet (0 meter) og etter 10 sekunder står 10 meter unna, så har du gjennomsnittlig hatt farten 1 meter per sekund. Går du med farten 1 meter per sekund vil du i løpet av 10 sekunder ha gått nettopp 10 meter. Skriver vi dette opp matematisk kan vi skrive

\(\text{Fart} = \frac{ \text{Endring i posisjon} }{ \text{Tid} } = \frac{ (10 - 0)   \ \text{meter} }{ 10 \ \text{sekunder} } = 1 \frac{ \text{meter} }{ \text{sekund} }\)

 

Så hva er da egentlig akselerasjon?

Jo, akselerasjon er egentlig ikke noe mer mystisk enn endring av fart. På samme måte som at fart sier hvor mye [enheten til posisjon] endrer seg per sekund ([meter] per sekund, eller m/s) noe om endringen av posisjon, så sier akselerasjon hvor mye [enheten til fart] endrer seg per sekund, altså [enheten til fart] / s, eller [m/s] / s. Man kan lese dette som meter per sekund (fart) per sekund. Og da slår man ofte sammen de to per sekund så det blir per sekund i annen.

Et eksempel der vi kanskje har intuisjon om akselerasjon kan være når vi sitter i bil. Hvis vi sitter i en Tesla og står i ro (farten er lik 0 meter per sekund), og har en av de dyre Tesla'ene, så oppgir de at du kan akselerere fra 0 km/t til 100 km/t (ca 28 m/s) på 2.6 sekunder. Så endringen av fart er (28 - 0) m/s, og tiden er 2.6 sekunder. Setter vi det inn i liknende formel som vi hadde over blir det

\(\text{Akselerasjon} = \frac{ \text{Endring av fart} }{ \text{Tid} } = \frac{ (28-0)\ \text{meter per sekund} }{ 2.6 \ \text{sekunder} } = \frac{28}{2.6} \frac{ \text{meter per sekund} }{ \text{sekund} } = 10.77 m/s^2 \).

 

Akselerasjon er altså endring av fart, eller for å være helt korrekt så er det endring av hastighet. Man skulle kanskje tro at dette er bare tullepirk, men det er det faktisk ikke, fordi fart er liksom bare hvor fort det går (i en eller annen retning), mens hastighet også sier noe om at man beveger seg i en spesifikk retning. Dette er jo litt viktig når man for eksempel flyr. Hvis man skal til USA holder det ikke at man flyr i 1000 km/t hvis man flyr rett syd, liksom.

Det betyr også noe når man skal se på hva som skjer hvis man kjører i sirkel. Hvis man skal kjøre i en sirkel skal man alltid være like langt vekk fra midten. Det går an å ha lik fart hele tiden, men da må man hele tiden forandre hastigheten, fordi i en sirkel går det aldri rett frem - banen bøyer seg jo hele tiden. Når hastigheten forandrer seg betyr det at det er en akselerasjon der. For sirkelbanen kalles denne sentripetalakselerasjon. Og nå kommer det jeg ikke er så veldig glad i - jeg skal nemlig bare oppgi formelen for sentripetalakselerasjon uten noe mer forklaring, eller utledning, da:

\(a=\frac{v^2}{r}\)

 

Grunnen til det er at for å komme frem til denne formelen så trenger man litt mer matte enn det alle har hatt i skolen som er obligatorisk (man trenger vektorregning).

Forklaringen på symbolene er at a selvfølgelig er akselerasjon, v er hastighet, og siden det er \(v^2\) så er det hastighet ganget med seg selv, og r er radiusen i sirkelen (avstanden fra sentrum av sirkelen til der du er). Så hvis du f. eks. kjører i en sirkel med 20 m/s (72 km/t), og denne banen har en radius på 100 meter så blir sentripetalakselerasjonen

\(\frac{(20 m/s)\cdot(20 m/s)}{100 m} = \frac{400 \frac{m^2}{s^2}}{100 m} = 4 \frac{m}{s^2}\)

 

Et triks jeg pleier å bruke er å sjekke om enheten blir riktige til slutt, og her ser vi at det blir riktig fordi vi fikk \(\frac{m}{s^2}\).

Det høres kanskje litt rart ut at man kan kjøre med en helt jevn fart rundt i sirkelen, og allikevel så har man en akselerasjon, men det er jo fordi du endrer hastigheten din til å peke i en annen retning. Det er er derfor du kjenner at du liksom blir dyttet utover når man svinger med bilen. Det er også derfor sentrifugering i vaskemaskinen virker, fordi klærne (og vannet i klærne) snurrer kjempefort rundt i sirkelbane og blir dyttet inn mot kanten. Det er da små hull som gjør at vannet sklir gjennom og ut, mens klærne blir litt tørrere hele tiden.

 

1

Publisert 1 kommentar til Ukens formel: nøytrontettheten i en reaktor

 

Ukens formel kommer på søndag, og grunnen til det er rett og slett det at den siste uken har vært fryktelig travel, med å forberede leiligheten (jada, boring, med så mye mas om dette, still true, though) - på toppen av alt måtte jeg plutselig hive meg rundt og rydde kalenderen fri på torsdag og fredag for å filme med Telia. Og det er grunnen til at jeg ikke fikk til formelfredag på fredag, og at det kommer i dag istedetfor - please forgive me (og tusen tusen takk til de fine nuktek-studentene som syntes det var helt greit å flytte forelesningen sin fra fredag 10-12 til mandag 8-10, selv om det kjennes som om vi skal møtes alt for tidlig i morgen akkurat nå 😛 ) ♥

- oppskrift -

Ok! Ukens formel gikk jeg igjennom da jeg foreleste nukleær teknologi nå på onsdag, og det er formelen for tettheten av nøytroner i en reaktor. Nøytroner er jo veldig viktige, fordi det er de som får alt til å skje i reaktoren... Formelen ser sånn ut:

- hva det betyr -

n står for nøytroner - hvor mange man har. Først, på den venstre siden av er lik-tegnet står det n(t) (som man leser som n av t), som betyr at antall nøytroner kan komme til å forandre seg når tiden går - så det er altså ikke like mange nøytroner hele tiden. På høyre siden står det \(n_0\) (som man leser som n null), som betyr så mange nøytroner man har liksom til å begynne med.

k er kritikalitetsverdien til reaktoren, som var den jeg snakket om i forrige formelfredag.

1 er tallet 1;)

t er tid, og måles i sekunder (tid måles alltid i sekunder i fysikk-formler - som jeg nevnte i s=vt-innlegget).

l er gjennomsnittlig levetid for et nøytron - som her betyr hvor lang tid tar det fra et nøytron blir "født" i en fisjon til det er spist opp - enten i en kjerne som fisjonerer igjen, eller i en eller annen annen reaksjon, i en kjerne som ikke fisjonerer

 

- fremgangsmåte -

hvis k = 1 så spiller det ingen rolle hva t eller l er, for da blir det uansett \(e^0\) som er lik 1, og \(n(t)=n_0\) - dette betyr at antall nøytroner er konstant, hele tiden lik det det var da vi begynte. Som jo er det man ønsker 🙂

Men, hvis det er en bitte liten endring, feks at k blir 1.001 istedetfor 1 - hva kan det egentlig ha å si?

Hvis \(n_0\) er 1000 og l=0.084 sekunder (det er typisk sånn det er i en godt designet standard reaktor), og vi vil se hvor mange nøytroner det er etter ett sekund blir \(n(1) = 1000\cdot e^{ (1.001-1)\cdot\big(\frac{1}{0.084}\big)} = 1012.\)

Dette betyr at hvis reaktoren har en effekt på 1 megawatt, og det da er denne lille fornadringen i kritikalitet (k), så går effekten opp til 1.012 megawatt på ett sekund, og det er helt uproblematisk og fint og flott. Det er sånn skal det være en normal, godt designet reaktor...

I Tsjernobyl var ting litt annerledes; den var jo ikke så veldig godt designet (med mindre hovedmålet ditt var å produsere våpenplutonium, og sikkerheten til de som jobbet der ikke var så kjempeviktig - da var den KJEMPEBRA designet). I Tsjernobyl-reaktoren var det nemlig sånn at l ble ganske mye mindre enn 0.084 sekunder. Der var gjennomsnittlig levetid for nøytronene nemlig 0.0001 sekunder, og da blir ting litt annerledes: da øker nemlig antall nøytroner med ca 22000 ganger på ett sekund, og effekten går fra 1 megawatt til 22000 megawatt på samme tid. Ja, du gjetter riktig; den økningen er eksplosiv :/

Nå skal jeg bare tømme (det nesten tomme) vinglasset mitt, så er det kvelden på meg her i alle fall. Siden jeg skal forelese klokken 8 i morgen så holder det ikke bare å faktisk være oppe og på plass - jeg bør liksom være uthvilt og på i tillegg...hashtag foreleserliv, liksom.

God natt ♥

 

2

Publisert 2 kommentarer til Svar på spørsmål om nøytroner og forrige formelfredag

Hei fine ♥

Jeg får jo masse gode spørsmål fra dere lesere, og jeg har lyst til å bli mye flinkere til å svare på disse! Noe av poenget med sosiale medier er jo nettopp at de skal være, vel, sosiale - altså at kommunikasjonen ikke bare går én vei. Nå er jeg akkurat ferdig med å forberede meg til forelesningen jeg skal holde i morgen tidlig, og jeg ser at akkurat NÅ rekker jeg å presse inn et lite svar på et spørsmål jeg fikk etter forrige formelfredag 🙂

Er det et mål å senke farten på nøytronene? Er det det man kaller å få dem inn i "thermal spectrum"?
Gir lavere fart/energi større sannsynlighet for at de treffer fissilt materiale? Relevant for alle reaktortyper?
Ja, det er et mål å senke farten til nøytronene! Når nøytronene "fødes" har de VELDIG høy energi (1000000 elektronvolt), mens vi ønsker å bremse dem ned til bare 0.025 elektronvolt. Når de har denne energien (0.025 elektronvolt) kalles de for termiske nøytroner, og det er helt riktig at når du har alle (de fleste) av nøytronene med denne energien så kalles det for et termisk spektrum  (thermal spectrum på engelsk, ja 🙂 ). Grunnen til at vi ønsker å bremse ned nøytronene er fordi sannsynligheten for at de skal få en atomkjerne til å fisjonere blir så UTROLIG mye større - faktisk kan fisjon bli 10 000 ganger mer sannsynlig! Så det er ikke det at det er mer sannsynlig at nøytronet treffer en kjerne når det har lav energi, men energien bestemmer hva slags reaksjon som mest sannsynlig skjer når den treffer en kjerne. Feks så kan nøytronet bare bli spist opp og lage avfall hvis det ikke får kjernen til å fisjonere, og dét ønsker vi jo i alle fall ikke... Nedbremsing av nøytroner er relevant for de fleste reaktortyper, men man kan også lage det som her raske reaktorer (fast reactors), og hvis du har en sånn type så vil du absolutt IKKE bremse nøytronene - disse fungerer altså på en annen måte enn de såkalte termiske reaktorene, som bremser nøytroner til et termisk spektrum.

Han som sendte spørsmålene over hadde noen flere ting han lurte på også, men siden de ikke handlet om akkurat dette med at nøytronene skal bremses ned så tar jeg de heller en annen dag - nå trenger jeg rett og slett skjønnhetssøvnen så jeg er ship shape for studentene klokken 9 i morgen 😉

Forresten: Se det nydelige bildet fotografen tok av utsikten vår i går! Han har virkelig klart å fange den stemningen vi har her vi sitter i stuen, hver eneste kveld - og det er jeg så glad for, for den er bare magisk ♥

(Foto: Trond Walsø)

Edit: Da jeg skrev innlegget i går var jeg ganske sliten, etter en lang dag, og endte opp med å skrive feil tall på energien til nøytronene i det de "fødes". Jeg hadde skrevet 200000000 elektronvolt, mens det riktige tallet er rundt 1000000 - som jeg har rettet opp i teksten nå. Ikke at det hadde noe å si for det jeg skrev ellers i denne teksten (poenget er at de har veldig høy energi, og at de skal bremses ned til lav energi), men rett skal jo liksom være rett, da 😉

Publisert Legg igjen en kommentar til Hva skjer i reaktoren? (Firefaktorformel)

Denne ukens formelfredag MÅ jo bli en liten oppsummering av forelesningen jeg holdt i nukleær teknologi tidligere i dag: Firefaktorformelen (som ved en feil først ble skrevet Fire4faktorformelen nå - og det er vel nesten sånn jeg burde fortsette å skrive den 😛 ). Vi bretter opp ermene, selv om det er fredag, og går rett på sak!

 

- oppskrift -

Firefaktorformelen er, som det vel nesten sier seg selv, en formel som består av fire faktorer - altså fire forskjellige tall/verdier som ganges sammen (faktorer er ting som ganges sammen). Den er enkel og grei på formen, og ikke vanskelig å bruke i det hele tatt, og den ser sånn ut:

og med ord så blir det k uendelig \((k_\infty)\) er lik epsilon \((\epsilon)\) ganget med p ganget med f ganget med eta T \((\eta_T)\), for det står et usynlig gangetegn mellom faktorene, som man vanligvis ikke skriver. Jeg har faktisk ikke vært konsekvent på om jeg skriver gangetegn eller ikke her på bloggen innser jeg, for forrige ukes strekning og fart og tid skrev jeg med gangetegn, mens formelfredag for to uker siden, som handlet om Newtons andre lov, skrev jeg uten gangetegn... Vel vel, da er det i alle fall forklart, og det er lov å skrive uten å ta med gangetegnet 🙂

 

- hva det betyr -

På venstre siden av likhetstegnet står k uendelig, og dette kalles for nøytron-multiplikasjonsfaktoren (for en uendelig stor reaktor). For å holde tunga rett i munnen: nøytron-multiplikasjonsfaktoren forteller om det blir flere eller færre nøytroner i en reaktor, så det er altså forholdet mellom hvor mange nøytroner som fins etter den nåværende generasjonen med fisjon sammenliknet med hvor mange det var i forrige generasjon.

Hvis k er større enn 1 så betyr det at det skjer mer og mer fisjoner i brenselet, og reaktoren løper løpsk. Hvis k er akkurat 1 (som den skal) så er reaktoren kritisk, og det betyr at den er balansert og alt er fint og flott, og det er like mye fisjon som skjer hele tiden. Hvis k er mindre enn 1 så betyr det at det skjer mindre og mindre fisjon i brenselet, og hele kjedereaksjonen slutter og reaktoren skrur seg av.

På høyre side av likhetstegnet står det først \(\epsilon\), som er hvor mange nøytroner som vil gå rett og gi rask fisjon (fast fission factor), og dermed flere nøytroner totalt sett. Neste  faktor er p, som er hvor mange nøytroner som blir spist opp av brenselet mens de egentlig skal bremses ned (resonance escape probability), så her blir det færre nøytroner. Faktor nummer tre er f, som forteller hvor mange termiske nøytroner som faktisk blir spist opp - så selv om nøytronene har overlevd til den energien som gir høyest sannsynlighet for fisjon så vil allikevel en god del bli spist opp i ikke-brensel (thermal utilization). Til slutt er det \(\eta_T\), som forteller hvor mange nøytroner man får for hvert nøytron som treffer en spaltbar kjerne, altså som treffer en kjerne i det som faktisk er brensel.

- fremgangsmåte -

Hvis vi starter med 1000 nøytroner, så skal det fortsette å være 1000 nøytroner totalt etter hver eneste generasjon med fisjoner i brenselet.

Eta kan feks være 1.04. Det betyr at det blir 1000 nøytroner ganget med 1.04 = 1040 nøytroner. Videre kan p være 0.8, som gjør at av de 1040 nøytronene er det bare 1040*0.8 = 832 som overlever det å bli bremset ned til lav energi. De andre blir "spist opp" av uran-238 (hovedsakelig) på veien. Deretter kan f være 0.799, som betyr at 832*0.799 = 655 - altså at det er 655 nøytroner som faktisk gir fisjon i brenselet. De andre nøytronene (832-655 = 167) blir "spist opp" av kjølevæske og kontrollstaver og uran-238 (forskjellen fra den forrige faktoren er at nå er det snakk om de nøytronene som har fått riktig energi, mens den forrige faktoren handler om hva som skjer på veien fra høy energi til riktig, lav energi), som altså ikke fisjonerer. Den siste faktoren er \(\eta_T\), som forteller hvor mange nøytroner som kommer ut for hvert nøytron som går inn i en fissil kjerne (altså uran-235). \(\eta_T\) er faktisk ikke det det samme som hvor mange nøytroner man får fra hver eneste fisjon, for \(\eta_T\) tar også med i beregningen at en liten del av de nøytronene som treffer uran-235-kjernen vil bli spist opp, og noen vil gjøre andre ting. Hvis \(\eta_T\) = 2.02 blir det 655*2.02 = 1323 nøytroner.

1323 er åpenbart mer enn de 1000 som var til å begynne med, så det kan virke som om de tallene jeg har satt opp gir en kjedereaksjon som løper løpsk. MEN! Firefaktorformelen tar ikke med en siste, viktig faktor - nemlig hvor mange nøytroner som forsvinner ut av reaktoren (det er ikke så lett å passe på alle nøytronene hele tiden). Det er det som ligger i \(k_\infty\), altså en uendelig stor reaktor - for hvis reaktoren er uendelig stor vil jo heller ingenting noensinne kunne forsvinne ut av den. I vikeligheten er selvsagt ingen reaktor uendelig stor, og man må derfor også ta med at en viss del av nøytronene som produseres vil forsvinne.

Hvis sannsynligheten for at nøytronene skal bli i reaktoren er 0.7559 (det vil si 75.59%), eller, sagt på en annen måte 24.41% av alle nøytronene forsvinner ut av reaktoren, og da er de bare tapt :/ Når vi trekker fra de 24.41% som forsvinner, så sitter vi igjen med like mange nøytroner som vi startet med, og kjedereakjsonen er balansert og kritisk og veldig fin ♥

 

Bildet under viser nettopp forskjellen på en kritisk kjedereaksjon til høyre - altså at én fisjon i gjennomsnitt gir én ny fisjon, mens det er en overkritisk kjedereaksjon til venstre - altså at én fisjon gir feks tre nye fisjoner og hver av dem gir tre nye igjen...

PS: Et kjernekraftverk kan aldri eksplodere som en atombombe! Altså, den kjedereaksjonen som skjer i et kjernevåpen kan ikke skje i et kjernebrensel 🙂

PPS: Goood helg nydelige mennesker ♥♥♥

3

Publisert 3 kommentarer til Formelfredag: strekning, fart, og tid

Fredag er formeltid, og etter å ha satt i gang med flere forskjellige, som jeg har lyst til å dele med dere, innså jeg at det er umulig å gå noe videre før jeg har tatt denne klassikeren... Den kalles vel ofte for veiformelen og er like liten og søt som Newtons 2. lov (jeg lovet å følge opp med en del ting fra det forrige innlegget om den andre loven, men vi må rett og slett ta en del ting i riktig rekkefølge, så ikke alt bare blir tøys og tull, og vi må ha denne før vi kan gå videre 😉 )

Den er en klassiker fordi alle bruker den mer eller mindre bevisst hele tiden, og dessuten lurer jeg på om mange lærer den allerede på barneskolen (jeg gjorde i alle fall det). I denne formelen så betyr s strekning, v er for fart, og t er for tid, og fra denne kan man altså regne ut hvor langt (hvor lang strekning) man kommer når man har en viss fart i en viss tid.

For eksempel: Du har en fart på 20 m/s i 1500 sekunder. Da er \(v = 20 m/s\), og \(t = 1500 s\), og \(s = 20 m/s \cdot 1500 s = 30000 \) meter, også kjent som 30 kilometer 😉

Så kommer et veldig viktig NB! Hvis ting skal bli riktig i fysikken så kan vi ikke bruke km og timer, men vi må bruke meter og sekunder. Det er det som kalles standard enheter, og det er meter/sekund (m/s) for fart, sekunder for tid, og meter for strekning.

Men det er ikke noe vanskelig å gjøre om fra kilometer per time til meter per sekund 🙂 Hvis du for eksempel kjører i 50 km/h: For det første vet vi at én km er det samme som tusen meter, og da blir 50 km det samme som 50000 meter. For det andre vet vi at én time er det samme som 3600 sekunder (en time er 60 minutter, og i hver minutt er det 60 sekunder - \(60\cdot 60=3600\) 😉 ). Dermed blir 50 km/h det samme som \(\frac{50000 m}{3600 s}\) (den brøkstreken betyr jo bare at man skal dele på hverandre), så da blir det altså \(\frac{50000}{3600} m/s = 13.9 m/s\) 🙂

Hvis du heller vil vite hvor lenge det er til du er fremme, er det tiden (t) du vil finne. Hvis det for eksempel er 10 km (10000 m) igjen, og du kjører 15 m/s (54 km/h) blir svaret på hvor lang tid det tar: \(t = \frac{s}{v} = \frac{10000 m}{15 m/s} = 667 s \approx 11 \) minutter.

Eller hvis du vil vite hvor fort du må kjøre så tar det strekningen (avstanden) og deler på tiden - bare husk husk husk på å bruke meter og sekunder og m/s, så går alt bra.

Denne formelen er det bare å kose seg med - noe du som sagt antageligvis allerede gjør 😉

Forresten, tusen takk for alle som har kommet med formelønsker - de kommer til å komme, jeg bare innså at nå var det en del ting som måtte gjøres i riktig rekkefølge her... Men jeg lover at det kommer både Einsteins formler og gassformler og alt mulig - fortsett gjerne å komme med ønsker! God helg ♥♥♥

5

Publisert 5 kommentarer til Ukens formel: Newton’s andre lov

Hei fineste lesere ♥ Ukens formel skal egentlig komme på fredager, men denne uken har jeg en ganske god unnskylding/forklaring på hvorfor jeg ikke fikk det til før nå: Denne uken skjedde det nemlig noe litt uvanlig (uvanlig som i noe man ikke gjør så ofte) - Anders og jeg ble plutselig eiere av ny og større leilighet! Vi har hatt en ganske intens leilighetsjakt nå den siste måneden pluss litt til, der vi visste at nå måtte vi finne noe, før Anders må gå in i sin PhD-innspurtsperiode, og vi plutselig ikke kan gjøre noe før om et år igjen. Så, plutselig på onsdag ettermiddag fikk vi tilslaget 😀 Hele torsdagen satt jeg i møte med Kjerneelementgruppen og diskuterte hva som skal være det viktigste man skal lære i naturfag i fremtidens skole, og på fredag hadde jeg en del arbeid å ta igjen på Blindern (siden jeg hadde vært to dage borte, i møter), og på fredag kveld måtte vi faktisk ut og feire leilighetskjøpet. I går morges dro vi på familietreff til Rendalen, og først nå kom vi hjem igjen, og endelig kommer ukens formel (uken er jo tross alt i over ennå 😉 ):

Jeg har faktisk gledet meg til jeg skulle ta tak i akkurat denne - en av de aller fineste, nemlig Newton's andre lov. Denne formelen (eller loven, som den kalles) er selve grunnsteinen i hele fysikk og beskriver hvor mye farten til en ting forandres (den akselererer) hvis man dytter på den med en kraft. Denne tingen kan være en bil, en pappeske, deg selv, eller et for eksempel et romskip. Man kom seg faktisk til månen med Newton's andre lov!

Den er egentlig bitteliten og veldig fin og søt og ser slik ut:

Newton's andre lov F=ma

F betyr kraft (force), m betyr masse (hvor tung), a betyr akselerasjon. Massen og akselerasjonen ganges med hverandre. Vi pleier å si "F er lik m ganger a". På overflaten til jorden så faller alle ting med samme akselerasjon, 9.81 \(m/s^2\) (enheten er meter per sekund i annen, og forklaringen av hvorfor det er denne rare enheten kan komme i et annet innlegg hvis det er interesse for det), alltid! Det er egentlig litt rart 🙂 Hvis du går inn i et lufttomt rom og slipper en tung kule og en lett fjær, så faller de faktisk akkurat like fort. Dette er ikke egentlig så veldig intuitivt, fordi vi sjelden er i lufttette rom, og da faller jo ikke en fjær og en kule like fort - men det er luft(motstanden) som gjør at fjæren faller saktere. I denne videoen er faktisk Brian Cox i et lufttett rom, og han slipper en bowlingkule og fjær samtidig... (me loves ♥ it):

Med Newton's andre lov kan vi regne ut hvor mye kraft jorden trekker på deg som menneske. Hvis du veier for eksempel 70 kilo (massen din er altså 70 kilogram) kan vi finne kraften jorden trekker på deg til å være

\(F = ma = 70\cdot 9.81 N = 686.7 N\). Bokstaven N betyr Newton som er enheten til kraft. Masse har enhet kilogram, akselerasjon har \(m/s^2\) og kraft har enhet Newton.

Hvis du hopper i fallskjerm blir du altså dratt nedover så du går fortere og fortere. Men når du står stille på bakken, så akselerer du jo ikke videre nedover mot jordens sentrum, og det er fordi bakken dytter deg oppover akkurat like mye som jorden drar deg nedover, slik at du står helt i ro. Hvis du hadde stått på månens overflate ville du også stått i ro, men månen trekker ikke like hardt på deg fordi den er mindre enn jorden. Derfor ville du, selv om massen din er 70 kg, veid mindre på månen enn du gjør på jorden! Faktisk veier du omtrent 6 ganger så mye på jorden som på månen. Dét betyr at musklene ikke trenger å være så sterke lenger.

 

Enda verre blir det hvis man er vektløs i verdensrommet slik som man er på den internasjonale romstasjonen (ISS, International Space Station). Å være vektløs er egentlig ganske dumt for mennesker og er grunnen til at astronauter kan få muskelsvinn ved å være i verdensrommet. Musklene blir ikke så mye brukt. Nå ser det ut til at vi mennesker kommer til å dra til Mars etterhvert, og da er det fint å finne på noe lurt så astronautene ikke mister alle musklene sine (da blir det tristefjes i romskipet). En løsning er å late som at man har gravitasjon.

Som jeg skrev over så drar jorden deg nedover med 9.81 \(m/s^2\) (det blir mindre og mindre når man drar vekk fra jorden i romskipet). Hvis vi nå får til å få denne akselerasjonen i romskipet så vil det kjennes ut som helt vanlig gravitasjon. Det er faktisk ikke mulig å skille gravitasjon og akselerasjon, og dette var noe Einstein kom på og kalte ekvivalensprinsippet.

Men å akselerere et romskip med 9.81 \(m/s^2\) koster ganske mye energi og gjør at man går fortere og fortere, noe som ikke nødvendigvis er lurt hvis man skal til Mars (da må man jo også bruke masse energi på å bremse). En måte å løse dette på er å lage kunstig gravitasjon i romskipet...

 

2

Publisert 2 kommentarer til Ukens Formel: Eksponensiell vekst

Hei fredag, og hei igjen fredagsspalten (som har hatt veeeldig lang ferie nå 😉 ), nemlig Ukens Formel ♥ Sist gang jeg presenterte ukens formel handlet det om halveringstid som forklarer hvordan man finner ut hvor mye Uran (eller andre radioaktive stoffer) man sitter igjen med hvis man starter med for eksempel 1 tonn og venter 4.5 milliarder år (dette er jo nesten jordens alder).

Denne gangen skal vi snakke om søsteren til halveringstidsformelen, nemlig formelen for eksponensiell vekst. At noe vokser eksponensielt betyr at hvor mye det vokser med er en prosentandel av hvor mye du har. Dette kjenner vi godt igjen fra når man bruker kredittkort og ikke betaler. Et typisk kredittkort har rente på omtrent 20% i året. Dette betyr at hvis du låner 10000 kroner og ikke betaler tilbake, skylder du 2000 kroner ekstra det neste året (veksten er 2000 kroner), og låner du 100000 kroner vokser gjelden med 20000 kroner. Veksten er altså avhengig av hvor mye du har (det er det som menes med at den vokser proporsjonalt 🙂 )!

Halveringstidsformelen er egentlig bare en spesialversjon av den mer generelle formelen for eksponensiell utvikling. Den ser slik ut:

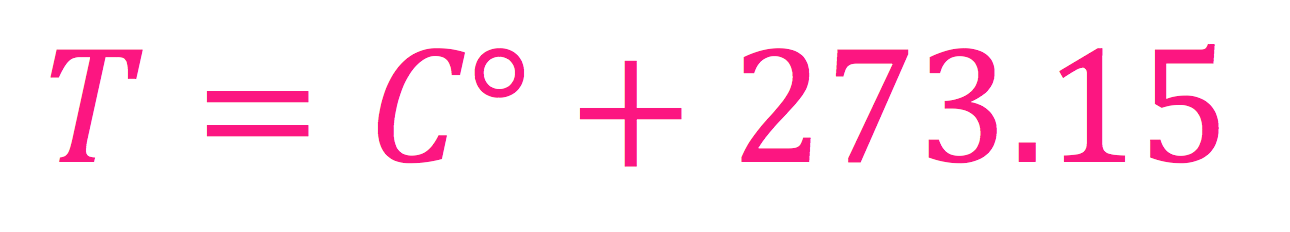
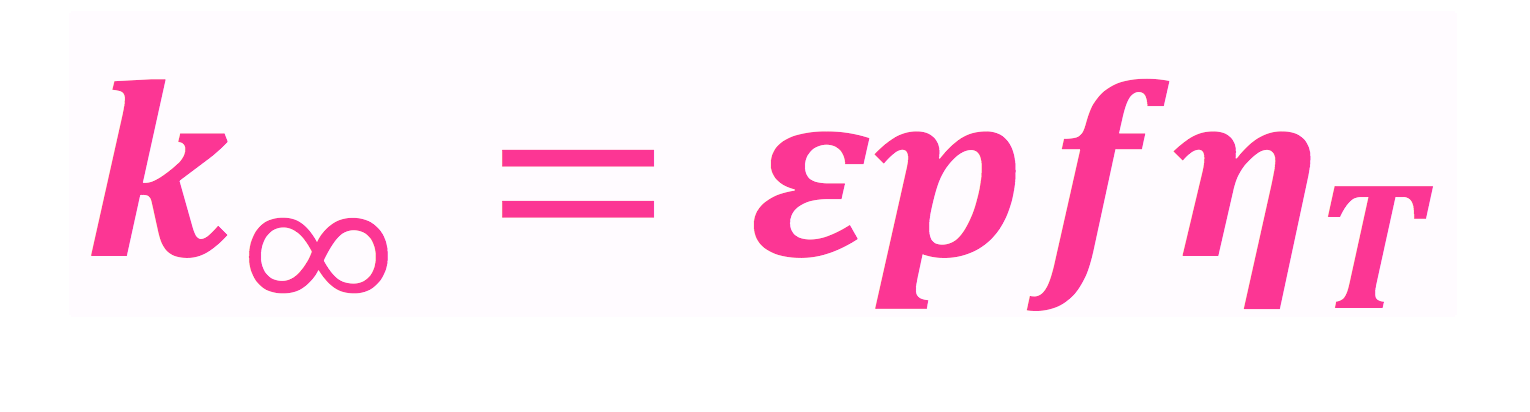
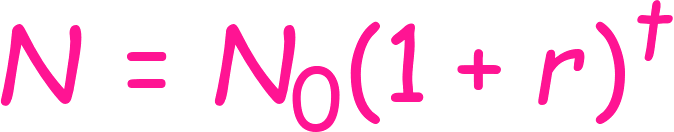På samme måte som i formelen for halveringstid er

  • N0 hvor mye du starter med (for eksempel 10000 kroner)
  • r er vekstraten (renten)
  • t er hvor lang tid det går (ofte antall år)
  • N er hvor mye du har til slutt

Siden renten fra kredittkortselskapet ofte er i prosent må vi dele det tallet på 100 for å sette inn i formelen (20% er 0.20), og altså få vekstraten. Så for å ta eksempelet over med 100000 kroner:

\(N = 100000\cdot(1+0.20)^1 = 100000\cdot 1.20^1 = 120000\), altså 20000 kroner mer enn vi startet med. Vi kan nå finne ut hvor mye vi skylder etter 10 år ved å sette inn 10 i stedet for 1, og da betyr det at man må ta det tallet som vi får inni parentesen (i dette tilfellet så er det 1.20) og gange med seg selv 10 ganger:

\(N = 100000\cdot(1+0.20)^{10} = 100000\cdot 1.20^{10} = 100000\cdot 6.19 = 619173\), over en halv million mer enn det vi lånte. Så med eksponensiell vekst så går det liksom fortere og fortere, og det er litt kjedelig med renter når du skylder mye penger - i alle fall hvis renten er høy, sånn som med kredittkort 😉

Etter 4 år så har gjelden altså doblet seg - fra 10 000 til 20 000. Så, etter (ca) 4 år til har den doblet seg én gang til - da fra 20 000 til 40 000, og hvert 4. år (ca) blir gjelden dobbelt så høy som det den var... :/

Denne formelen blir brukt overalt hvor vekstraten er proposjonal med hvor mye du begynner med. I biologi (og medisin så klart) ser man ofte på bakterievekst eller andre mikroorganismer der vi ser eksponensiell vekst. I USA ser det ut til at befolkningen over de siste 100 årene er godt beskrevet av eksponensiell vekst med 1.5% vekstrate.

PS: noen reagerer kanskje på at formelen er i den flotte(?) fonten "comic sans"... Vel, denne fonten er faktisk ganske mye brukt blant fysikere rundt omkring i verden, blant annet av fantastiske Fabiola da hun annonserte at de hadde funnet Higgs på CERN. Hvis fonten er bra nok for Fabiola, er det bra nok for meg ♥