Hopp til innhold

4

Publisert 4 kommentarer til Formelfredag: Pytagoras

Søndag kveld allerede? Det har gått ganske i 100 denne helgen; vi har hatt både Andrea og Arian (fien niese og nevø) på overnatting, og de dro for ikke aå alt for lenge siden. Veldig veldig hyggelig, men tiden går jo, og det blir litt ekstra opprydding... Uansett, nå får det holde med Formelfredag-tørke, og jeg er heldigvis godt innafor med Formelfredag/ukens formel nå - det er tross alt nesten tre timer til klokken vipper midnatt, og det offisielt er en ny uke 🙂

Ukens formel er en VIRKELIG klassiker, nemlig Pytagoras' formel, og jeg syns rett og slett vi bare bretter opp ermene, og går rett på sak:

 

Oppskrift

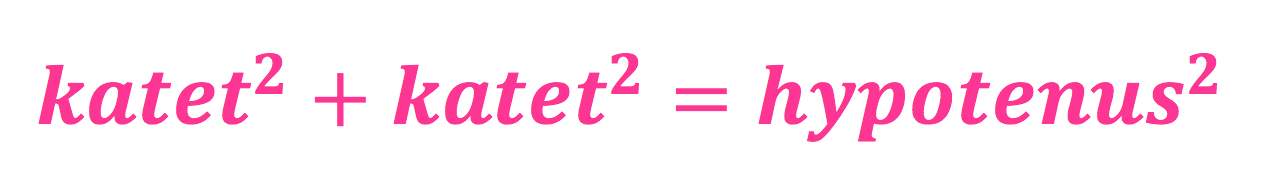
Hva det betyr

For å forklare hva denne oppskriften faktisk betyr trenger vi å se på trekanten under:

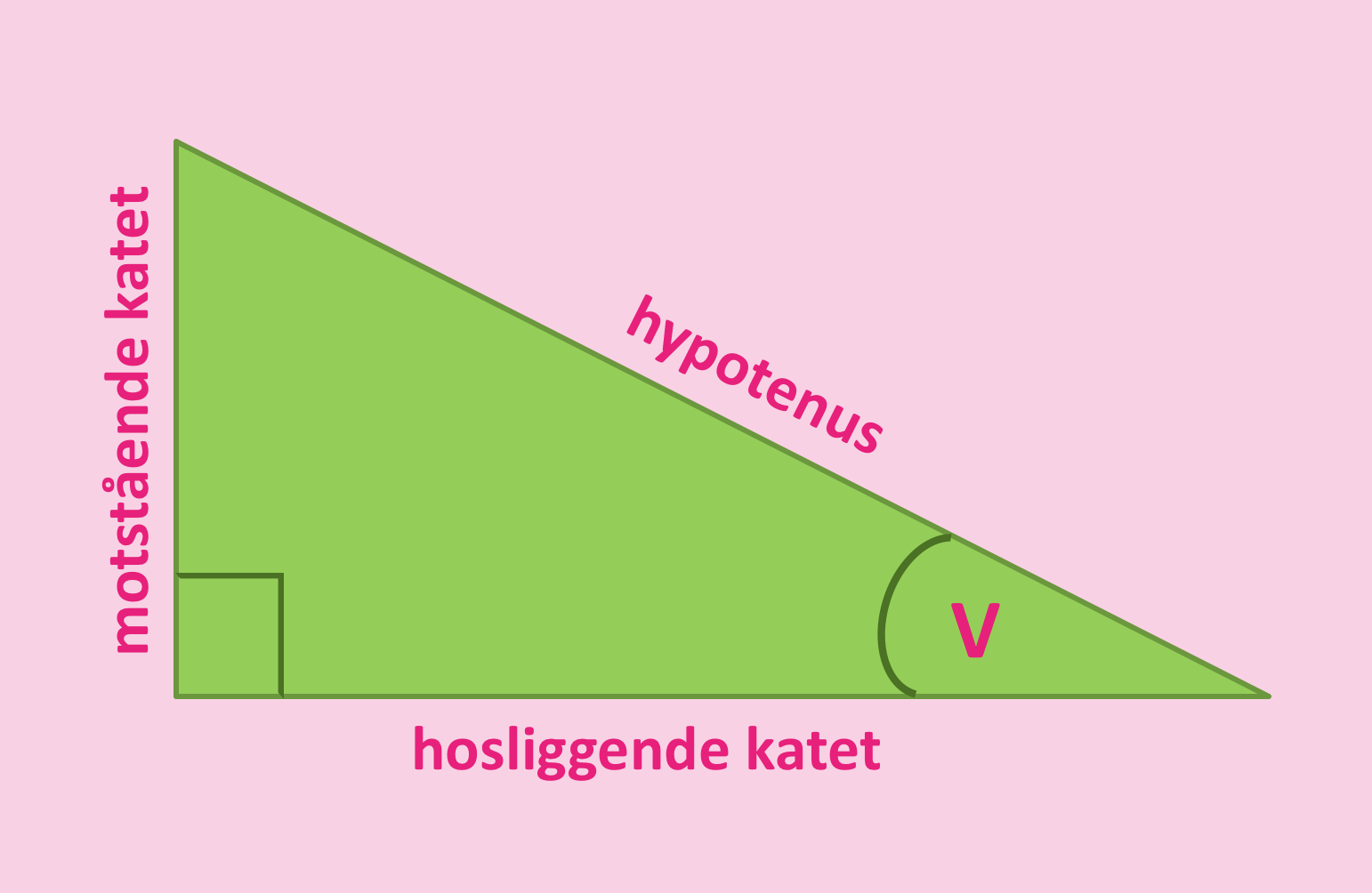
Det som er spesielt med denne trekanten er at den er en såkalt rettvinklet trekant, som betyr at den ene vinkelen (den nede, i venstre hjørne) er rett. At en vinkel er rett betyr at den er 90 grader, og man markerer at en vinkel er akkurat 90 grader med å tegne et sånt hjørne over den, som jeg har gjort 😉 Pytagoras handler om sånne, rettvinklede trekanter.

Denne trekanten har, som alle trekanter (rettvinklede, og andre), tre vinkler; altså to i tillegg til den rette vinkelen. I figuren min har jeg markert en av de to andre vinklene - den nede i høyre hjørne. Jeg har gitt den det flotte navnet "V" (jeg kunne ha kalt den, feks, "flippetiflopp", men det er mer vanlig å kalle vinkler for "V" - det er også enklere og raskere å skrive). Men poenget i selve Pytagoras-oppskriften er ikke disse vinklene; det er de tre sidene er det som er viktig. Vi trenger dog å markere vinklene for å vite hvilke av de tre sidene det er vi snakker om...

Den lengste siden i trekanten, som går fra "V" og til den siste vinkelen, som jeg ikke har snakket om, og som er navnløs, heter "Hypotenus". De to andre sidene heter "Katet", men som du kan se på figuren min så heter den ene "Hosliggende katet" og den andre "Motstående katet". Det med hosliggende og motstående har å gjøre med "V". Den som er "hosliggende" er ved (hos) den vinkelen som heter "V", og den som er "motstående" står altså "mot" "V".

Det med at den ene kateten heter hosliggende, og den andre heter motstående er egentlig ikke viktig akkurat nå med pytagoras; men det kommer til å bli viktig neste uke, og derfor tenkte jeg det var like greit å bare ta det nå med én gang - litt rettvinklede treknater-lærdom der, altså ♥

\(katet^2\) betyr katet ganget med katet (altså at kateten skal ganges med seg selv), og \(hypotenus^2\) betyr hypotenus ganget med hypotenus (hypotenus ganget med seg selv). Først tar man den ene kateten og ganger med seg selv, så tar man den andre katenten og ganger med seg selv, og dett er altså det samme som hypotenusen ganget med seg selv (hvis noen lurer på hvorfor jeg ikke sier noe om areal, så er det med vilje, og det kommer en annen dag, og hvis du ikke tenkte på areal i det hele tatt så kan du bare se bort fra denne parentesen 😉 ).

Fremgangsmåte

Så lenge vi vet hvor lang to av sidene i en (rettvinklet) trekant er, så kan vi regne ut hvor lang den siste siden er med Pytagoras.

Hvis feks den ene kateten er 5 cm, og den andre kateten er 3 cm, så blir hypotenusen:

\(5\cdot5+3\cdot3=hypotenus^2\), og videre blir det  \(25+9=hypotenus^2=26\)

Siden \(hypotenus^2\) er 26, så blir hypotenusen hvadratroten av 26: \(\sqrt{26}\)=5.099. Hvis du ikke har en kalkulator som kan regne ut kavdratroten av et tall så har du faktisk det allikevel, det er bare å skrive sqrt(26) i søkefeltet i nettelseren 😀

Hvis vi vet hvor lang den ene kateten er, og hypotenusen, kan du finne den siste kateten. Hvis feks hyptenusen er 7 cm, og den hosliggende kateten er 6, så blir den motstående kateten:

\(6\cdot6+katet^2=7\cdot7\), og videre blir det  \(36+katet^2=49\). Så flytter vi 36 over til høyre siden av er lik-tegnet, slik at den kateten vi ikke vet lengden på blir stående alene: \(katet^2=49-36=13\). Da vet vi at den ukjente kateten (i dette tilfellet den motstående kateten) ganget med seg selv blir 13, og for å finne hvor lang den faktisk er så tar vi kvadratroten av 13: \(katet=\sqrt{13}=3.606\)

...og selvfølgelig brukes Pytagoras til masse, men det må bli en annen gang. I kveld holdert vi oss toil å bare se på hvordan formelen faktisk er, og hvordan man bruker den.

Bonus: Andy the Candy har en veldig fin (syns Anders og jeg, i alle fall) sang om Pytagoras. Hør den her ♥♥♥

 

 

4

Publisert 4 kommentarer til Den Stephen Hawking-teksten jeg sa jeg skulle skrive…

Link til Stephen Hawking-teksten er nederst i innlegget, i tilfellet du ikke vil lese journalist-rant 😉

På onsdag skrev jeg en oppdatering her på bloggen, fra en travel dag i Trondheim, som ikke ble mindre travel av nyheten om at Stephen Hawking dessverre var død. NRK Ytring var tidlig på ballen, og ville veldig gjerne at jeg skulle skrive en liten tekst om Hawking. Først sa jeg nei - ikke fordi jeg ikke ville, men fordi jeg ikke kunne se at jeg hadde tid til det (det var en uvanlig travel og slitsom dag), men etter litt om og men, sa jeg ja. Jeg hadde jo egentlig noe jeg gjerne ville si om Hawking 🙂

For å få til dette ryddet jeg unna arbeid - det vil si, utsatte det til senere (det er jo ikke som om det forsvinner, fordi det kommer noe du bare MÅ gjøre nå), og jeg ble nødt til å droppe boklanseringen til Henrik Svensen (Stein på stein. På sporet av den største masseutryddelsen i jordens historie); som jeg så gjerne skulle vært på, både fordi han er en bekjent og formidlingskollega (man støtter kolleger!), fordi han er dyktig, og ikke minst fordi jeg skal intervjue ham om boken hans om en måned... Da kunne det jo liksom vært ganske nyttig å få med seg et sånt arrangement. Men jeg droppet det altså, for å skrive tekst om Hawking.

Så kom jeg hjem på kvelden, etter en lang dag i Trondheim, var godt i gang med teksten, men langt fra ferdig, og fikk migrene. Sendte melding om dette til Ytring, at jeg ikke kom til å få skrevet noe mer på teksten den kvelden. Fikk svar om at det gikk fint, fordi Stephen Hawking kunne man skrive om også på torsdag (dagen etter at han var død).

Torsdag morgen fikk jeg på ny melding fra Ytring, som lurte på om jeg var bedre, og om jeg kom til å få skrevet. Jeg fortalte at jeg var i et møte fra 9-11, men at etter det så var planen å jobbe til jeg ble ferdig med teksten. Ingen innvendiger på dette. Litt før kl 14 fikk jeg en ny melding, fra en annen person  i Ytring, som lurte på når jeg trodde jeg skulle bli ferdig med teksten, at det begynte å haste litt. Jeg svarte med én gang at jeg skulle få den ferdig i løpet av en time.

Kl 14:30 (torsdag etter lunsj), mens jeg satt og gjorde finpussen på teksten fikk jeg melding om at det var for sent og at Ytring ikke var interessert lenger. Rett før jeg var ferdig og skulle sende dem teksten de så veldig gjerne ville ha, som jeg først sa jeg virkelig ikke hadde tid til å skrive, valgte de altså å droppe det. Takk for den, liksom.

Poenget, kjære journalister (ikke bare i Ytring, men overalt ellers også): Når dere spør sånne som meg om å skrive, husk at vi ikke er journalister! Akademikere er ikke trent i det å hive seg rundt og produsere en tekst på null komma svisj. Vi er heller trent i det stikk motsatte. For oss (nei, jeg kan jo ikke snakke for alle, men jeg tror jeg snakker for mange), så er det å skrive en tekst man ikke hadde noen planer om å skrive på et døgn utfordrende. Og hvis det fins en deadline, så må den i alle fall kommuniseres. "Det hadde vært fint å få teksten så raskt du klarer" er ikke å formidle deadline. Jeg vil veldig gjerne være med å bidra, og jeg elsker å formidle kunnskap, men akkurat nå føler jeg meg litt dårlig behandlet - jeg syns ikke det er greit å gjøre sånn. For meg tar det faktisk omtrent en full arbiedsdag (totalt) å produsere en sånn tekst; selv om det bare er rundt 3000 tegn, så skal jo de 3000 tegnene liksom være på riktig plass 😉

Ok, det var bare det jeg ville si. Takk ♥

HER er teksten min om Hawking - Dagbladet syns tydeligvis ikke det var "for sent" å skrive noen tanker om ham da det hadde gått mer enn ett og et halvt døgn etter at nyheten om at han hadde dødd ble kjent. De valgte til og med å spare teksten fra torsdag ettermiddag (da de fikk den) til i dag, lørdag, da den ble trykket både på papir og på nett 🙂

Neste gang går jeg nok direkte til Dagbladet.

9

Publisert 9 kommentarer til En liten tur til Trondheim, og 10 myter om stråling

I går var jeg på Nettverkssamlingen i realfag i Trøndelag (nå: Det ene fylket som heter Trøndelag, det fins ikke noe Sør- og Nord-Trøndelag lenger #samfunnsfagsfakta) og hokdt tre foredrag, for 300 realfagslærere. Det som er veldig gøy med det er at hvis hver lærer har 150 elever i snitt hvert å (og gitt at jeg når igjennom til hver lærer - det gjør jeg sikkert ikke, men forhåpentligvis ganske mange av dem 🙂 ) så betyr det at jeg indirekte er med å påvirke ganske mange elever, sånn bittelitt ♥

Det ene foredraget jeg holdt het 10 myter om stråling, og jeg tenkte jeg skulle ta noen av dem her:

♥ Strålingen kommer og tar deg. "Stråling" høres litt mystisk og magisk ut, men den kommer fra et eller annet stoff, og med litt kunnskap er det ikke vanskeligere å beskytte seg mot enn alle mulige nadre stoffer man ønsker å beskytte seg mot. Det er latså ikke sånn "you can't hide".

♥ Stråling er farlig – uansett – og nedfallet fra Tsjernobyl vil gi 500 ekstra kreftdødsfall i Norge. Lave doser av stråling ser ikke ut til å være farlig, og det fins ganske mye forskning som peker mot at lave stråledoser til og med kan være bra for oss (Google "hormese" eller "hormesis"). Å "regne seg frem til" at det blir 500 ekstra kreftdødsfall i Norge pga Tsjernobyl er 100% useriøst og uetisk.

♥ Utslippet av (radioaktivt) cesium fra Tsjernobyl-ulykken tilsvarer 100 Hiroshima-bomber. Det kan godt hende at det stemmer, men det er en ganske uinteressant opplysing. Dette utsagnet prøver å få oss til å tenke at Tjsernobyl er som 100 Hiroshima-bomber, noe som selvsagt ikke stemmer. Saken er at det som dreper i en atombombe-eksplosjon er hovedsakelig selve sprengkraften og den enorme varmen som produseres, og ikke cesium. Et annet poeng er at man ikke får dannet akkurat de samme stoffene når en atombombe eksploderer som man får i brensleet i et kjernekraftverk - utsagnet kan like gjerne bety "i en atombombe blir det produsert veldig lite cesium sammenliknet med i et kjernekraftverk".

♥ Flere millioner mennesker kommer til å dø som en følge av utslippene fra Tsjernobylulykken. Nei. Under 100 døde som en direkte konsekvens av strålingen, og de aller fleste har fått forholdsvis lave stråledoser etter Tsjernobyl, og trenger ikke leve i frykt pga dette. Man tenker seg at det kanskje vil bli 6000 ekstra kreftdødsfall pga ulykken - som absolutt er 6000 for mange, men ikke i nærheten av millioner, som jeg har sett enkelte påstå.

♥ Etter Fukushima-ulykken var det farlig å være i Tokyo pga høye strålenivåer. Nei. Selv da det var på det høyeste strålenivået i Tokyo, etter Fukushima-ulykken, var det lavere strålenivåer der enn det det er i feks Oslo hele tiden. Norge flyttet ambassaden sin vekk fra Tokyo under ulykken - hvis Japan skulle hatt samme "sikkerhetsmarginer" på sin ambassade i Norge, måtte de ha flyttet ambassaden sin ut av landet.

♥ Valget mellom kull eller kjernekraft er som å velge mellom pest eller kolera. Nei, det er jo ikke det. Hvis du feks sammenlikner dødsfall per terawattime produsert energi så er kull DESIDERT verst (161 døde/TWh), mens kjernekraft kommer ut bedre enn til og med vannkraft (0.04 døde/TWh). Fra kull får man utslipp av CO2, svovel, svevestøv...dessuten er asken som produseres fra et kullkraftverk radioaktiv. Faktisk får du en høyere stråledose ved å bo i nærheten av et kullkraftverk enn det du får ved å bo i nærheten av et kjernekraftverk. Et kjernekraftverk ville blitt stengt på dagen (etterfulgt av store overskrifter i avisene) hvis det hadde utslipp av radioaktive stoffer på samme måte som kullkraftverk har hele tiden.

Grunnen til at jeg ikke tar alle 10 mytene er at noen av dem krever litt mer skriving enn det jeg har gjort på hver av disse punktene. Hvis det er interesse for at jeg skal dele resten, så er det bare å rope ut, så skal jeg se hva jeg kan få til 🙂

Under er Trondheims-turen i bilder (i alle fall dag 1: fra Oslo til Trondheim), litt sånn time for time ♥

Tidlig morgen, hjemme, i sminkeprosessen.

 

Etter sminke, klar for Trondheim.

 

Alt man trenger å ha med for et døgn i Trondheim (nei, jeg kan ikke vite hva jeg kommer til å ville ha på meg på scenen dagen etter).

 

Kl 9: På kontoret først, siden flyet ikke går før på ettermiddagen.

 

Jobber med foredrag nummer to.

 

Jobber med foredrag nummer tre.

 

Kaffe!

 

Te... Jeg prøver å variere litt, så det ikke blir så iiiinmari mange kaffekopper i løpet av en dag, og så syns jeg Pukka-teene er veldig fine - jeg blir litt glad av eskene, faktisk 🙂

 

Kl 14: Setter nesen mot Gardermoen.

 

Elsker den roen jeg får etter å ha sjekket inn, når jeg har godt med tid før flyet går, selvsagt. Setter meg ned med et glass vin, og boken til Henrik - et sånt tilfelle der vin og jobb faktisk kan være i skjønn forening 😉

 

Siste jobb på foredrag 2 på flyet. Sitat fra den siste rapporten til FNs klimapanel.

 

Kl 1930: Fremme!

 

2

Publisert 2 kommentarer til Stephen Hawking er død

Hei alle ♥ Jeg er en rask tur innom her for å si hei, og beklage mitt fravær, og sørge for at det ikke blir totalt fravær i dag også. I skrivende stund sitter jeg på Værnes, drikker et glass vin, og forsøker å skrive en tekst om Stephen Hawking. Jeg er i Trondheim fordi i dag har holdt tre foredrag, for 300 realfagslærere, og nå er jeg altså ferdig, og skulle helst bare sittet og drukket vinglasset og stirret ut i luften og "tømt" hjernen.

Men fysiker Stephen Hawking døde tidlig i dag tidlig; den 14. mars - pi-dagen, og Einsteins bursdag. Mens jeg sto og snakket ringte telefonen, igjen og igjen, og det rant inn med meldinger. Det meste sa jeg nei til, men NRK Ytring klarte å overtale meg til å skrive en tekst om Hawking og mitt forhold til ham... Jeg tror en hovedgrunn til at så mange visste om ham var at han var en fantastisk formidler, og når jeg selv snakker så varmt om vitenskapsformidling, hvordan kan jeg da si nei når formidling om en formidler er ønsket? Jeg landet altså på ja, selv om bildet under (som ble tatt da jeg kom meg på hotellrommet i går kveld) egentlig er en god illustrasjon av hvordan jeg føler meg akkurat nå. På toppen av alt så kom jeg på at jeg hadde en annen deadline i dag, som jeg helt hadde glemt - det ser derfor ut til at jeg rett og slett må droppe boklanseringen til Henrik Svensen i kveld, men sånn er det noen ganger. Jeg får jo uansett snakket med Henrik når jeg skal intervjue ham om boken hans 🙂

Jeg kommer sterkere tilbake i morgen!

4

Publisert 4 kommentarer til Tusen takk!

Kjære alle, fine mennesker som har sendt meg meldinger, forslag, tilbud, etter at jeg fortalte at jeg hadde sagt opp jobben for en uke siden - TUSEN TAKK! Jeg blir så glad og rørt over at så mange klapper og heier, og det føles rett og slett ganske fantastisk ♥

Så er det jo de (som heldigvis ikke er mange, men jeg har møtt et par) som ser på meg som om jeg har falt ned fra månen, og sier: Ja, men hva er planen med dette? Har du sagt uten å ha en ny jobb?!? (Som om jeg er den aller mest un-employable personen noen sinne - og det er det jeg får litt lyst til å svare også, liksom Shit, tror du ingen kommer til å ville ansette meg, ever again...? ). Svaret er jo at nei, det fins ingen "plan" eller "strategi", annet enn at jeg kom til et punkt der det eneste riktige for meg var å si opp, og at jeg vil ha det gøy. Oppsummert er altså "strategien":

  1. "Måtte" si opp
  2. Ha det gøy

Jeg har naturlig nok noen tanker om veien videre, men de kan jeg ikke dele her på bloggen før tiden er inne. Det er jeg sikker på at alle forstår ♥ Det som er sikkert er at jeg ikke kommer til å forsvinne, og jeg kommer til å blogge videre om "reisen", pluss kjernefysikk og forskning og sånn, selvsagt 😉 (I midten av april skal det gjøres et eksperiment på plutonium, som er ca en direkte videreføring der min doktorgrad sluttet - jeg kommer SELVFØLGELIG til å være med, og, ja, jeg skal blogge om det 🙂 )

The only way to do great work is to love what you do

Dette sitatet fra Steve Jobs oppsummerer egentlig alt, og er det én ting jeg har fått 100% klart og tydelig for meg så er det at Steve Jobs har meget rett i dette. Men dét er jo også en all right lærdom å ta med seg, er det ikke?

Nå i oppsigelsesperioden er jeg så utrolig heldig at jeg får lov til å være på Realfagsbiblioteket, og jeg har den første dagen min der i dag. Oppdrag 1: Den 16. april skal jeg intervjue Henrik Svensen om den nye boken hans, som heter "Stein på stein", som visstnok handler om både geologi og forskning. Så nå har jeg fått boken i hånden, og skal kose meg med å lese. Det jeg vet er at Henrik er en utrolig dyktig formilder (han har feks vunnet Forskningsrådets formidlingspirs), så jeg er sikker på jeg kommer til å kose meg - pluss at geologi antageligvis er det realfaget jeg kan minst om, så jeg er gira på å lære masse! På baksiden av boken står det blant annet:

Jorden for 252 millioner år siden: En planet i krise. Enorme vulkanutbrudd. Dyr og planter som bukker under, et ødelagt ozonlag og et surt og livløst hav. Slik har det vært her. På jorden. Før oss.

Mine første tanker: I den store sammenhengen er det omtrent ingenting som betyr noe - det syns jeg egentlig er litt deilig 😉

Publisert Legg igjen en kommentar til Hjemme med Anders

Endelig er han hjemme igjen, og det føles absolutt aller aller best ♥
Han er kanskje ikke den morsomste å være sammen (hei sliten etter lang reise, og jet lag) men han er her, og det er viktigst! Dessuten så får han vært med på Olav Thon-prisutdeling og -galla i morgen, og det er jeg utrolig glad for. LA ligger jo 9 timer bak oss, så han er i alle fall jet lagged den riktige veien med tanke på festligheter i morgen - med mindre han våkner midt på natten og absolutt ikke får sove igjen, da...men han har uansett lovet å være med i morgen 🙂

Og apropos Thon-tilstelningen: Dresscoden er smoking, og det kommer til å gå ganske slag i slag for meg i morgen (skal jo til Hamar og holde foredraget Jeg hater ordet "naturlig"), så jeg må være smart når det kommer til outfiten. Jeg kommer tilbake til Oslo ikke så lenge før vi skal være nede i Universitetsaulaen, og dermed må man ha en plan for å få dette til å funke smooth.

Mitt triks i sånne sammenhenger er å fikse håret i en klassisk frisyre på morgenen, og å legge opp til en sminke som egner seg med kraftig farge på leppene. Jeg kommer også til å ha på meg skjørt eller kjole, slik at jeg kan ha på meg strømpene jeg trenger på kvelden, hele dagen. Dermed blir jeg festpyntet på et blunk ved å slenge på stor ørepynt, dra på meg lang kjole og høye hæler, og ta på meg en knall leppestift (jeg har ikke landet på om det blir knall rosa, eller rød - det blir nok feelingen i det øyeblikket jeg skal ta den på som bestemmer, og siden kjolen min i morgen er sort så passer jo alt). Min go to-frisyre i denne typen situasjon er stor, pen (i motsetning til messy, altså) hårtopp. Jeg tror kanskje jeg lager den langt nede i nakken i morgen, men det er i alle fall sånn type som på bildet under. Med briller, perler i ørene, og en dus farge på leppene blir det perfekt for foredrag, og med statement-smykker og sterk farge på leppene blir det perfekt for fest 🙂

Da jeg fant frem dette gamle bildet, for å vise frisyren, "kom jeg på" at jeg har denne røde jakken - den hadde jeg liksom helt glemt... Tror jammen jeg må ha på meg den i morgen. Det er deilig med litt farge, og rødt på Kvinnedagen er jo perfekt!

Alt sånt er liksom enklere for mennene: Det står "smoking", så da tar du på deg smoking, liksom. Tror jeg har en bra plan nå, da, og jeg gleder meg til i morgen - både til foredrag og Thon-prisen!

 

Publisert Legg igjen en kommentar til 5 fine ting jeg skal gjøre denne uken

Gårsdagens "avsløring", om at jeg har sagt opp jobben på UiO, er selvsagt ikke noe som "bare skjedde" (hverken avgjørelsen eller innlegget). Å gå til det skrittet at jeg faktisk sa opp en fast jobb i Staten har vært noe jeg har tenkt nøye over, og beslutningen har jeg omsider landet på etter å først å ha tenkt den første tanken i slutten av oktober i fjor. Det har selvsagt ikke vært lett, og jeg har vært mye lei meg.

Så nå er det deilig at dagene er blitt BETYDELIG lysere (det er IKKE mørkt selv om vi går hjemmefra slik at vi er på AKS i det de åpner om morgene :D) ute, og at vi tross alt er i den første vårmåneden (nei, da, det kjennes ikke heeelt sånn ut ennå - men det kommer, plutselig!), og nå "eier" jeg jobbsituasjonen. Nå løfter jeg blikket og ser fremover, og her er fem fine ting jeg skal gjøre denne uken:

Tirsdag: I morgen skal jeg være med i panelet på MNKOM-lunsj, sammen med Kristian Gundersen og Gunn Hild Lem. Vi skal diskutere om formidling av kunnskap kan være (helt) nøytral. Det skjer klokken 12:15-13:00 på Realfagsbiblioteket - kom kom 🙂

Onsdag: Anders kommer hjem fra USA igjen! Dette er den siste turen over dit nå mens han holder på med doktorgraden, og nå gleder jeg meg til å ha han hjemme, lenge, igjen ♥

Torsdag: Først på torsdag setter jeg nesen opp mot Hamar, der jeg skal holde foredrag for Norsk Fjørfelag, om hvordan Jeg hater ordet "naturlig" (og når jeg er ferdig med det må jeg seriøst sette meg ned og skrive kort og informativt om dette foredraget, og få lagt det ut på Athenas-profilen min - virkelig, altså!). Torsdag kveld er det utdeling av Olav Thon-prisene, pluss galla. En liten filmsnutt av kjolen jeg tenker å ha på meg ligger ute på snapstoryen min (sunnivarose), for de som har lyst til å ta en kikk 🙂

 

Fredag: Da skal jeg (kanskje) i et spennende møte - med blikket festet fremover. Det er kanskje teit å dele, når jeg egentlig ikke deler noen ting, men jeg må på en måte ha det med allikevel... Spesielt etter at jeg i dag fikk kommentaren hva er liksom strategien din med å si opp uten å ha en ny jobb?!? Kanskje ikke ment som noe annet enn ren nysgjerrighet, men når man er litt der jeg er nå så kan alt tolkes negativt (:P), og da er det deilig at spennende, dyktige folk gjerne vil møte deg, og akkurat dét har jeg lyst til å dele; nei, jeg har ingen klar plan, men ja, det skjer ting (kanskje) 🙂

Eller skal uken brukes til både tenking og skriving.

Dette bildet er fra doktorkreeringen, i juni, oi fjor, og selv om bildet ikke er nytt nå, så syns jeg det passer fint for temaet å se positivt på fremtiden 🙂 

 

Det har altså vært en lengre periode der jeg har fokusert mye på det som er negativt i livet, og nå er det jammen deilig å fokusere på ting som er positive. Mer av det fremover ♥

3

Publisert 3 kommentarer til Jeg har sagt opp

Den 15. august 2003 gikk jeg med ærefrykt inn i Store Fysiske auditorium, Fysisk institutt, UiO, satte med på første rad, og hørte på professor Gunnar Løvhøiden snakke om horror vakuui (tror det var sånn han skrev det).

Mandag denne uken, den 26. februar 2018, sa jeg opp jobben min på UiO, og den 31. mai 2018, etter nesten 15 år på Universitetet i Oslo (7.5 år som ansatt) er jeg ferdig. 

Jeg vet ikke hvor veien går herfra. Bare at den går et sted. Det er både skummelt, trist, rart, og spennende.

♥♥♥

Publisert Legg igjen en kommentar til Ukens spørsmål: Fisjon eller fusjon?

Det. Er. Så. FANTASTISK. DEILIG. Å kjenne solen varme ansiktet, og  se den faktisk smelte snø og is. Himmel! Selv om Anders dro til LA i dag, som selvsagt gjør meg litt trist (hvor ble det av superselvstendige Sunniva, egentlig? Kanskje hun egenltig aldri fantes – og bare dukket opp midlertiidg, da det var absolutt nødvendig...?) så blir jeg så mye mer glad av solen og «varmen», at totalen i dag helt klart er positiv. I skrivende strund er Anders i en Dreamliner et eller annet sted over Atlanteren, og jeg sitter hjemme ved spisebordet vårt. Som nevnt i går er jeg kjempestolt av han – han er virkelig helt fantastisk dyktig (i tillegg til å være snill, kjærlig, og en super stepappa).

Men apropos solen: Jeg fikk tilsendt et bilde på mail her om dagen, med spørsmålet vil du kalle dette fisjon eller fusjon? Jeg trodde først at dette var fra en elev som ville ha meg til å gjøre leksene for seg (det skjer nemlig, og det er selvsagt helt uaktuelt), så jeg svarte rett og slett du ser vel hva som står skrevet?

Så fikk jeg svar tilbake

Jo men akkurat i dette trinnet, omdannes jo helium til helium, og to lettere grunnstoffer. Dette er jo definisjonen på fisjon?

Tenkte at dette er jo et kjempebra spørsmål, og svaret er at nei, dette er ikke fisjon – det er bare et trinn i fusjonsprosessen. Det som skjer her er at du helt riktig har to helium-kjerner, som blir til en ny heliumkjerne, men denne er tyngre - to lette kjerner har gått over til å bli en tyngre, altså. Samtidig blir det to protoner (hydrogen-1, som er det som vises her, er kun ett proton) til overs. Dette er en del av fusjonsprosessen, og ikke en egen prosess der du feks har helium som deler seg i to og blir hydrogen - da ville jeg vært enig i at det var fisjon 🙂

Totalen her er at to lettere kjerner smelter sammen (fusjonerer) til å bli én tyngre kjerne, pluss to overskuddsprotoner.

Energien som kommer her i denne reaksjonen er fra nettopp fusjonen av lett helium til tyngre helium, og ikke fra helium som splitter seg til protoner - for den reaksjonen gir på ingen måte energi. Den koster energi. Hvis man har en kjerne som er så tung som uran (eller egentlig noe som er tyngre enn jern) så kan man få energi på å fisjonere (spalte i to).

Ga dette svaret noen mening? Eller, altså, svaret er at dette er fusjon, og det er jo greit nok, men ga forklaringen noen mening...?

Uansett så håper alle har nytt denne dagen like mye som meg ♥

Publisert Legg igjen en kommentar til Bra damer, og den beste dagen på lenge

Hei verden ♥ Dagen i dag har bare rett og slett vært...bra. Den beste på lang tid, egentlig! Selv om jeg ikke er glad for at Anders reiser til LA igjen i morgen, da. Heldigvis er han bare borte to uker denne gangen, så det skal gå ganske greit å holde ut 😉 Dessuten så er jeg veldig glad for grunnen til at han reiser; nemlig at han har fått lov til å holde et foredrag på en av de store (viktige) konferansene - sånn er forskerlivet, og det vet jeg. Også må jeg jo bare si at det er en skikkelig god følelse å være stolt av kjæresten sin. Virkelig!

Podcasten "Bra Damer" av Guri Solberg, der jeg var gjest for ca to uker siden er forresten ute nå:


I intervjuet snakker jeg blant annet Louboutins (disputasskoene, altså, for de som ikke har fulgt meg så nøye så lenge) og om modeller og forenklinger av naturen - hva er det som er "riktig" nivå av forenkling, liksom. Jeg må jo si jeg ble ordenltig glad da jeg i dag tidlig fikk en hyggelig melding fra en som hadde sittet og hørt på podcasten og sa at hun aldri hadde tenkt over nettopp dette med at alt vi gjør er jo en eller anne modell og forenkling av virkeligheten, og at hun likte det jeg sa...det gjør meg glad, da 🙂

Jeg innrømmer at jeg skvatt litt av det aller siste spørsmålet jeg fikk, men det var virkelig gøy å få være med. Guri Solberg er ordentlig dyktig! Dere kan høre hele podcast-episoden HER - håper dere liker det ♥